Appendix I: Fundamentals of Thermodynamics
Table of Contents
Properties of a Substance and the State of a System
Pure Substances and Simple Compressible Substances
The Entropy Balance and Lost Work
The First Law and Second Law Combined: The Two Availability Functions
Overall Availability Analysis of Earth
Example of Burning Methane and Octane
Introduction
The term thermodynamics is used in different ways – not without some controversy. What we have chosen to call thermodynamics includes all of what Clifford Truesdell [1] would call thermomechanics. Thermomechanics is divided immediately into classical thermodynamics or classical thermomechanics and rational thermomechanics as espoused by Truesdell and others. Even when I (Wayburn) was an undergraduate (mid 50s), professors liked to complain that, since we would consider systems in equilibrium only (or approximately so), we should call our course of study thermostatics. I tend to agree, but tradition prevails here as elsewhere. The term thermodynamics should have been reserved for irreversible thermomechanics, which, if we consider situations not too far from equilibrium, would be termed first-order thermomechanics, with higher-order versions of our science reserved for increasingly difficult cases. Thermostatics, then, is zeroth-order thermomechanics. But, this is just taxonomy. (Despite the advisability of knowing what one is talking about, the authors have no intention to limit this discussion to the names of things.)
Truesdell quipped that the reason classical thermodynamics is not understood is that it is not understandable. Occasionally, we shall point out situations that remind us of Truesdell’s remark. We shall never get out of this appendix without encountering something hopelessly confusing. Nevertheless, without departing far from “classical thermostatics” (or by grossly simplifying such departures), we shall provide ourselves with an improved conception of this much maligned subject. We will try to avoid telling unforgivable lies by inserting appropriate notes and disclaimers where they belong. That said, let us proceed in our attempt to fathom the “unfathomable”. We would like to thank the many experts with whom we have exchanged correspondence and conversation; however, to avoid the risk of forgetting someone, we shall name no one. They know who they are. Wayburn takes sole responsibility for the mistakes. I hope our readers will not be shy about pointing them out.
Some Useful Definitions
The Control Volume
In classical thermodynamics one typically divides the universe, which, for the purposes of a particular problem, may be a small portion of the real Universe, into the system and the surroundings. A system may be either closed or open. A closed system is a fixed amount of matter under investigation. An open system is an identifiable region in space, normally containing matter but into which and out of which matter may flow. The surroundings are everything else in the “universe”. In our treatment, following Van Wylen and Sonntag [2], we shall refer to an open system as a control volume and, normally, we shall retain the term control volume even when no matter crosses the boundary of the control volume, i.e., even when the quantity of matter is fixed as in a closed system. Occasionally we will refer to the system, which may be open or closed.
[Note in proof (6-1-96): The solution of some problems is facilitated by partitioning the control volume. Sometimes additional insight is gained. For example, on p. 215 in Van Wylen and Sonntag [2], we are given a problem where the system is said to be a cylinder containing steam at 100°C that is engaged in heat transfer (to be defined below) to the surroundings, which are taken to be the ambient air at 25°C. Clearly, if the steam in the cylinder is at 100°C and the surroundings is at 25°C, Van Wylen and Sonntag have left something out of the formulation of the problem, namely, the region in space where the air or the wall of the cylinder takes on every value of temperature between 100°C and 25°C, which must exist because conductive heat transfer is taking place and which, according to the authors, is not part of the system and, also, not part of the surroundings. Thus, this classical division of the universe into two parts only, namely, the system and the surroundings, will not work. (Score one for Truesdell.) The moral of the story is that we must be suspicious of even time-honored received wisdom. The problem can be restored to reasonableness by admitting two parts to the system: the steam at 100°C and a region surrounding the steam that experiences a temperature gradient between 100°C and 25°C that accounts for the heat transfer.]
Clearly, the concept of control volume is slightly abstract. The boundary of the control volume is called the control surface; it is whatever we imagine it to be, except that it should be closed (not having any tears or holes in it) and orientable (having a distinguishable inside and outside), and need not correspond to the actual surface of a material object. The control surface may alter with time and the control volume may be hurtling through space at the speed of light if we imagine the control volume to contain a single photon, for example. Typically, in engineering, the control volume might be the interior of an automobile cylinder, part of the boundary of which, viz., the surface of the piston, is in constant motion during a thought experiment. The control volume might be disconnected if, for example, we take it to be the volume occupied by all the rain drops in a rainstorm; nevertheless, each component of the control surface is closed and orientable. It is this abstractness that makes the control volume and control surface such powerful concepts. Normally, everything that is outside the control volume is taken to be the surroundings, but in some problems it is convenient to consider more than one control volume or, equivalently, to partition the one control volume [as in the note above]. This is a departure from Van Wylen and Sonntag.
Properties of a Substance and the State of a System
In classical thermodynamics, as opposed to classical mechanics or statistical mechanics, we take substances to be pure continuous stuff in the Aristotelian sense; that is, we neglect the atomistic nature of matter and the individual motions of its particles to arrive at some sort of average properties. For example, the pressure of a gas in a closed container corresponds to the exchange of momentum of the individual molecules with the walls of the container. Rather than solve the equations of motions of the individual particles or compute the average using statistical methods, normally we measure the pressure with a single pressure gauge (neglecting even the differences in hydrostatic pressure due to the presence of a gravitational field) or assign a single quantity to be the pressure in a thought experiment.
Gas in a closed container is said to consist of a single phase. When we heat ice, it changes from a solid phase to a liquid phase to a gaseous phase. The liquid phase doesn't have a distinguished name; we call it simply liquid water. The gas phase is called steam or water vapor and the solid phase is called ice. Many of us are not aware, though, that water is found in eight separate solid phases. So when Kurt Vonnegut coined the term ice nine in his book Cat's Cradle, he knew what he was talking about. Our guess is that he had been instructed by his famous brother, Bernard Vonnegut, who had done the pioneering work on cloud seeding to make rain. Most pure substances exhibit only one gas phase and one liquid phase, but multiplicity of solid phases is common. Mixtures, such as oil and water, frequently exhibit multiple liquid phases. (In the vernacular, oil and water don’t mix.) In any case, a phase is defined to be a quantity of matter that is homogeneous throughout. When more than one phase is present, the individual phases are separated by phase boundaries.
In each phase, the substance is characterized by various properties such as pressure, temperature, and density, as well as other important properties to be defined below. The properties define the state of the substance even though not all of them are independent. A property is defined as any numerical value that can be assigned to a homogeneous quantity of matter that does not depend on the prior history of the substance, i.e., a quantity that depends only on the state of the substance. Thus, properties characterize states and states determine properties.
Clearly, in order for a single number to represent a property of a fixed homogeneous quantity of matter it is necessary for the quantity of matter to be in equilibrium with respect to that property. Equilibrium refers to the absence of any tendency to change state spontaneously. For example, if a cylinder (control volume) contains two samples of air separated by a thin metallic diaphragm, one sample at a high pressure and the other at a low pressure, each sample (viewed as a separate control volume) may be in mechanical equilibrium before the diaphragm ruptures; but, immediately following the rupture, the air in the cylinder (the original control volume) is wildly unequilibrated. However, after a period of time has elapsed the air in the control volume is again in equilibrium and we may refer to the pressure of the system. Similarly, if we place a large block of metal, initially in thermal equilibrium with the surroundings (the kitchen) in an oven, the surface temperature of the metal will rise practically instantaneously while the temperature at the center will be considerably lower. If the system is the block, the system will not be in thermal equilibrium again until the temperature throughout is constant at the oven temperature. Until such time, we may not refer to the temperature of the block. Of course, we can compute the temperature at any point within the block as a function of time by solving the heat equation, but the heat equation is outside the scope of classical thermodynamics.
Finally, thermodynamic properties are either extensive or
intensive depending on whether or not the property depends upon the
amount of material present or not. For example, temperature is an
intensive property, but volume is an extensive property. If half of the
block of metal of the preceding paragraph is discarded (without any other
effect taking place), the temperature remains the same, but the volume is
divided by two. An intensive property can be derived from every extensive
property by considering the extensive property per unit mass or mole of the
substance. (A mole of a substance is a quantity of mass – measured in the
system of units employed by the analyst – equal to the molecular weight of the substance.
For example, a gram mole of water contains 18 grams, since the molecular weight
of water is 18, whereas a pound mole of water contains 18 pounds of mass.
A gram mole of any substance contains Avogadro’s number of molecules – 6.023
1023
molecules. The number of molecules in a pound mole will be greater, of
course. The case of a mole of photons is interesting as photons have no
mass. Nevertheless, zero is a quantity and zero is the quantity of grams
in a gram mole of photons, which still contains 6.0231023
photons.) If 1000 grams of water occupy a liter of volume, an extensive
property, then water has a specific volume of 1 gram per milliliter.
Specific volume is an intensive property.
Processes
A change of state occurs whenever one or more properties of a system change. When the state of a system changes we say the system undergoes a process. We would like to describe a process by a path that consists of a record of all the states through which the system passed during the process, but recall that we cannot characterize the state unless the properties are well-defined and the properties are not well-defined unless the system is in equilibrium. But, if the system is in equilibrium, it has no tendency to change; so how can it undergo a process? We shall extricate ourselves from this predicament by a compromise. We shall say that a system undergoes a quasi-equilibrium process if the changes are sufficiently gradual that the system approaches equilibrium at each stage of the process sufficiently closely for practical purposes. The operative word is practical.
Every scientific calculation involves approximations. Nothing can be measured with infinite precision. In fact, many processes, some of which occur at high speeds – such as the operation of a refrigerator (listen to it hum) – do approximate equilibrium closely enough that their properties can be represented on a graph. This graph, then, is an adequate representation of the path of the process and computations based upon it are good enough for engineering and science. Of course, for a process to be truly in equilibrium at every point on its path, the process would require an infinite period of time. Such processes are of little interest to engineers. Finally, if the process returns the system to the same state after a characteristic period of time, the system is said to undergo a cyclic process or simply a cycle.
Pure Substances and Simple Compressible Substances
If a substance has a homogeneous chemical composition, even though it may consist of more than one phase, it is said to be a pure substance, provided, of course, that each phase has the same chemical composition. Thus, water is a pure substance even when it appears as solid, liquid, and vapor simultaneously. In many applications, air may be taken to be a pure substance even though it is a mixture of several species. If the composition doesn't change during the process under consideration, the fact that air is really a mixture can be ignored safely. Often this results in a great savings in computation. The analyst must use judgment in determining when a composite substance may be considered pure.
In many processes, surface effects, electrical effects, magnetic effects, elastic effects, etc. are not important. In this case, the only form of work that will be considered can be computed from changes in pressure and volume. Under these conditions, the substance is said to be a simple compressible substance and the expressions for derived properties in terms of fundamental properties are especially simple as we shall see in the section on the First Law. Remember, as in much of thermodynamics, whether or not a substance can be classified as a simple compressible substance depends upon the circumstances as well as the substance.
Balance Equations
The Generic Balance Equation
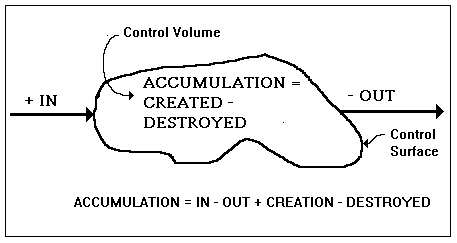
Figure I-1. The generic balance equation
The generic balance equation is so simple that, if we described it incorrectly to a three-year-old child, he or she would recognize that something was wrong, which is a good point in favor of the position that reasonableness is innate, i.e., an a priori synthetic judgment. One may argue as to what this equation may be applied to; but, if we should claim that it applies to what is commonly known as stuff, your objection would be a mere quibble. [Under the aegis of the commonality of the word stuff we consider both corporeal and incorporeal elements. For example, energy is conserved, however it may be more like the behavior of a mysterious something than the something that behaves. It may be so abstract that nothing but a mathematical mapping of the relevant portion of the Universe is adequate to describe it. Mathematicians are content to refer to this mapping as field equations. As far as they are concerned, the field equations are the phenomenon.
The generic balance (or accounting) equation states quite simply that the accumulation within the control volume equals whatever is created within the control volume minus whatever is destroyed inside the control volume plus whatever enters the control volume minus whatever leaves the control volume. The situation is illustrated in Figure I-1. By the accumulation we mean the difference between what we ended up with and what we started out with. This can be negative or positive; but, if it be negative, we might call its absolute value the deficit. As stated above, the control volume is any well-defined region in space. It may be changing shape and moving and it need not be a connected set.
[Note in proof (9-5-96): Many purists will object that the balance equations are not the laws of thermodynamics, which, according to natural philosophy, must be statements that come entirely from experience and may not employ such abstract concepts as energy, temperature, and entropy. In particular, the Second Law should be a statement about a particular type of physical device that cannot exist. In fact, we have two statements each with its own impossible device. We suggest that the reader consult the excellent book for the layman by P.W. Atkins [3]. This will not be our last mention of this book. Suffice it to say that the balance-equation approach is logically, if not philosophically, equivalent to the experiential statements of the laws.]
We now wish to describe the balance equations of thermodynamics, which we are giving the status of laws, the famous laws of thermodynamics. We shall describe the First Law first. Since the First Law is an energy balance, since everyone thinks he knows what energy is, and since entropy, which is an important property of thermodynamic systems, does not appear in the First Law, most thermodynamics texts do not define entropy before they discuss the First Law of Thermodynamics, which involves both work and heat. Work and heat are not properties of the system, but they are rather subtle concepts. Under some circumstances work and heat are mistaken for one another; whereas, if they are defined in terms of entropy, they can be distinguished easily – at least from the theoretical point of view. Therefore, we shall define and discuss entropy at this time. In our opinion, teachers of thermodynamics should give a little consideration to this departure from the usual way of presenting the First Law.
Entropy
Normally, students have a problem with the concept of entropy. This is expected, but what is unfortunate is that they think they understand energy. One supposes that if we use a term enough we think we understand it. After the population crisis and very much related to it, the most serious crisis facing humanity is usually referred to as the energy crisis – even by the President of the United States, high government officials, and famous professors. Of course it should be referred to as the entropy crisis, availability crisis, or emergy crisis, but we are getting a little ahead of ourselves. (It came as quite a shock to one of us when he discovered that the people who are running the world don't know what they are talking about – much less what they are doing.) To facilitate the definition of entropy without recourse to the Second Law, we shall depart from so-called classical thermodynamics, which forbids inquiry into the microscopic nature of the universe. Just for a moment, we shall take a quick peek at statistical thermomechanics.
Typically, a system the entropy of which we wish to know has
been defined in terms of common macroscopic thermodynamic properties that we
have at our disposal and with which the reader may already be familiar such as
volume, pressure, temperature, and internal energy for which we have not
given formal definitions. In addition, let us suppose that the analyst is
in possession (hypothetically) of a number of probability distributions Dk
= {pi, i = 1, 2, … ,Nk} each of which, k = 1, ... , M ,
(i) provides the probability 
that the system will be
found in the i-th microscopic state, and (ii) is entirely
consistent with the known macroscopic properties of the system.
Remember, in classical thermodynamics, we do not inquire deeply into the
microscopic picture; therefore; we should not be surprised to find that more
than one – perhaps many – such probability distributions could represent
precisely the same state viewed macroscopically. For each such
distribution a candidate Sk can be calculated for the entropy of the
system. It is the minimal amount of information – measured in bits, say –
to determine from the distribution under investigation the exact microscopic
state of the system. It should not be construed that this determination
could actually be carried out – even theoretically; but, it is easy to
determine the expected (in the probabilistic sense) information deficit
corresponding to the known macroscopic thermodynamic variables and the j-th
probability distribution
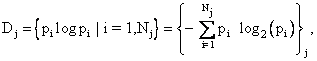
where Nj different possible and compatible microscopic states are associated with Dj . The macroscopic entropy of the system, S, is the maximum value of the minimal information deficits, i.e., S = maximum{Sj , j = 1 to M}, where M probability distributions are compatible with the macroscopic state of the system as described by classical thermodynamics. As a somewhat challenging exercise, the reader may show, by considering the old TV game Twenty Questions, that the minimal information to determine the exact microscopic state of the i-th microstate is the log to the base two of pi. This will give the entropy as the amount of information needed in bits, which would be converted into standard thermodynamic units by multiplying the same amount of information expressed as a natural logarithm
by Boltzmann’s constant, k = Ro/A, where Ro is the universal gas constant and A is Avogadro’s number. (Don’t worry if you don’t know what these numbers are.) The standard units of entropy are energy over temperature – essentially for traditional reasons. Despite the unfortuitous happenstance that Joules per Kelvin is not particularly suggestive of information, entropy is a measure of the quantity of information that would be needed to determine the microstate from the classical thermodynamic macrostate (except for a constant factor) although it is sometimes referred to as a measure of uncertainty, disorder, randomness, or chaos, which, from our view, are less satisfactory interpretations. [The preceding remarks on entropy are derived from Dr. David Bowman’s generous postings to a list server for physics teachers on the Internet.]
Let us continue our mathematical analysis for a simple and commonly encountered probability distribution. Suppose a system be capable of taking [capital omega] different quantum states with the probability for the i-th state being pi. Then, the entropy of that system is S = -k S pi ln pi , where S represents the summation from i = 1 to i = Ω, ln is the natural logarithm [ln pi is the exponent to which the transcendental number e (equal to approximately 2.718282) must be raised to get the number pi] and k is Boltzmann's constant. The case where the probability of each quantum state is the same, namely, when pi = 1/ Ω , is exceptionally famous. In that case, we get S = k ln Ω. The expression S = k ln Ω appears on Boltzmann's tomb – unless we have been hoodwinked by the scientific historians, which is not entirely out of the question, although Truesdell [1] provides a photograph.
We may now distinguish between heat and work, both of which entail the transfer of energy at the boundary and only at the boundary of a control volume; however, heat carries entropy along with it and affects the entropy balance accordingly. Work, on the other hand, carries no entropy, and, therefore, has no effect on the entropy balance. Because of this difference between heat and work an asymmetry arises; namely, work can be converted entirely to heat in every case including the case where no other change occurs in the universe, but heat can be converted completely to work only when the rest of the universe is changed in some additional fundamental way. If we restrict ourselves to cyclic processes, work can be converted completely to heat but not vice versa.
[Note in proof (10-15-97). This is easy to visualize: Case 1: Consider the spring escapement in your Grandfather’s watch. It transfers work to the gears, pointers, and whatever else accepts the work done by the spring mechanism, which we will take as “the system”. The state of the material objects by means of which this energy is transferred as work is completely organized. The microstate is completely determined by the extent to which the spring has become unwound. The probability of being in that state is one and the log of one is zero. The entropy is zero. Case 2: Imagine, for a moment, a hydraulic watch, say, driven by a pumped hydraulic fluid, which is permitted to flow across the control surface as we conceive it. This appears to be work too, but the turbulence and random motion of the pumped fluid as well as the friction losses in the pipe convert the electricity that drives the pump (work) into part work and part heat due to the turbulence and other forms of fluid friction. Since heat is crossing the control surface it will be accompanied by entropy since clearly the fluid will not be found in a state clearly defined by one parameter that takes its unique value with probability one. Case 3: Finally, if we had a steam clock, we could drive it by heating water in a boiler the surface of which facing the fire is our conceptual control surface. This is a case of heat and only heat crossing the control surface. Consider the entropy associated with this heat. Hint: Imagine how complicated fire is. The complications in the nature of the fire will complicate the conduction of heat to the boiler.]
[Note in proof (6-27-04). Some analysts may quibble that heat doesn’t cross the control surface. Rather, thermal energy crossing the control surface is heat; that is, crossing the control surface is part of the description of heat not separate from it. We do not feel the necessity for this kind of precision.]
The Energy Balance
The energy balance presented here is one statement of the famous First Law of Thermodynamics. We shall write the energy balance for the simplified case of uniform state and uniform flow. Uniform state means that each element of material inside the control volume has the same internal energy, u. The control volume is assumed to be homogeneous with respect to other physical properties as well. Despite the mysterious and abstract nature of energy, as noted above, the internal energy of a substance can be thought of (loosely) as the micro-mechanical energy associated with the internal motion and configuration of its molecules. It is like the calories in the food we eat. If the state be not uniform, we compute average values of the internal energy, u, and other properties using integral calculus. (It is standard practice to notate average properties by angle brackets, thus <u> is the average internal energy. We do not generally employ angle brackets as averages are clear from context.) Uniform flow means that the enthalpy, h, and other physical properties of incoming and outgoing flows of matter are constant across the area of flow and over the period of time under discussion. Enthalpy is internal energy plus the work that would be done upon the system by the material entering the control volume or the work that would be done on the surroundings by the material leaving the control volume. In the case of a simple compressible substance, one in which surface effects, electromagnetic effects, etc., are unimportant, h = u + Pv, where P is the total pressure of the system and v is the specific volume (the reciprocal of density). Enthalpy is more or less the internal energy of the gasoline about to enter an automobile engine plus the work done by the fuel pump to get the gasoline into the engine. Enthalpy is a trick devised by engineers to avoid accounting for this so-called injection work separately and, concomitantly, to account for the actual work done by the plant, which, of course, is its raison d'ętre, separately in the variable We so that it can be identified readily – uncontaminated by irrelevant contributions. Again, if the flow be not uniform, we employ the integral calculus. Many practical examples approximate the conditions of uniform state and uniform flow sufficiently well for engineering calculations.
A lay reader thought that enthalpy should be the internal energy minus Pv. She reasoned that doing work to enter the control volume erodes the energy. Yes, that it does, therefore we add Pv to get the enthalpy so that, when the substance has done the injection work, the internal energy alone remains. This gives the correct accumulation of energy within the control volume. For an excellent derivation of the formula for enthalpy see Van Wylen and Sonntag [2], 2cd Edition, SI Version, pp. 116-121.
The initials SI stands for Le Systeme International d’Unites, which is a version of the metric system that is very convenient for engineers and which enjoys international acceptance everywhere – except in the United States, which still employs the “British” system, long abandoned by Britain. As far as we Americans are concerned, it’s heartening to know that the international unit of energy is the joule. The international unit of power is one joule per second, i.e., the familiar watt. Also, we can write Newton’s Second Law of Motion now without a constant of proportionality (see note following this paragraph), or, if we wish to be obstinate, with a constant of proportionality equal to one. One Newton (N) of force equals one kilogram mass (kg) times one meter (m) per second (sec) squared, which last is an acceleration. Notice that, in SI, the unit of mass is the kilogram rather than the gram. One kilogram equals 2.2026 pounds.
Absolute temperature is measured in Kelvin (K) with the familiar
and typographically annoying degree sign neither written nor spoken. (We
say that 
. A Kelvin is the same size
as one degree Celsius, formerly denoted Centigrade, as the difference between
the freezing (triple?) point and boiling point of water under its own vapor
pressure is 100 degrees.) Since 2.54 centimeters (cm) equals one inch, a
foot is 30.48 cm or 0.3048 meters (m). Consequently, one meter is
3.2808399 feet, i.e., just over a yard. One liter is 1000 cubic
centimeters (approximately), thus one can compare metric volumes with American
volumes by simple arithmetic. Now, that wasn’t so bad was it? Of
course, now that the lesson is over, we shall probably employ American units
most of the time anyway.
Note. We wish to entertain the reader with one more subtlety with which he can embarrass many of his scientific friends. It is simply this: Newton’s Second Law is not F = ma . What can be said in general is that force is proportional to mass times acceleration. But, what is the constant of proportionality? Well, it depends on the system of units, doesn’t it. In the familiar British (American?) engineering system, it is called gc. But, it appears in the denominator, thus:
Now, force, F, is in poundsforce; mass, m, is in poundsmass; and acceleration, a, is in feet per second squared. Therefore, to obtain dimensional consistency, gc must have the units consisting of the ratio poundsmass per poundsforce multiplied by the ratio of feet over seconds squared. In this system,
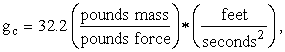
which is supposed to be (numerically equal to) the
average acceleration due to gravity at the Earth’s surface, hence the letter g.
(We suppose that the subscript c denotes constant. That is, gc is the same on the moon as it is on
Earth, although g, the actual acceleration due to gravity, is much
less. For all practical purposes, the acceleration due to gravity was nearly
constant so long as we had the good sense to keep our feet on the ground; but,
now that we have elected to break “God’s quarantine on mankind” provided by the
“vast distances between the heavenly bodies” [C. S. Lewis], gravitational
acceleration can hardly be taken to be constant. Nevertheless, 
,
which is a constant of proportionality – not an acceleration – is constant
everywhere.) Anyway, an object’s weight in poundsforce at the Earth’s
surface is numerically equal to its mass in poundsmass. Isn’t that
wonderful! Regrettably, this results in no end of confusion as to what
you weigh and what your mass is. Ironically, (many) engineers and (a few)
scientists are not spared. Just ask your favorite engineer what Newton’s Second Law of Motion is and let him explain the units. You may be in for
some fun. In the quasi-reasonable SI system, force has a name
different from the name for mass, but
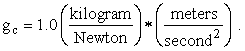
(Van Wylen and Sonntag [2] claim otherwise, namely, that in the SI system force is not an independent concept but rather is defined to be a kilogram meter per second squared. This is probably true, so I expect to get in trouble for sacrificing the elegance of one less fundamental concept for uniformity in the treatment of Newton’s Second Law of Motion.) One last thought: Please remember that (nearly) every equation in physics (as opposed to mathematics) is really two equations in one, both of which must balance, namely, an equation in numbers and an equation in units!
[Note in proof (7-30-97). In a private communication, Dave Bowman explained that, from the viewpoint of the theoretical physicist, many, most, or all of the so-called fundamental constants of the universe are really no better than conversion factors between unfortunate choices of units. For example, the speed of light in vacuum, c, is a conversion factor between (relativistic) intervals in units of time to units of length. If time-like intervals were measured in years, space-like intervals would be measured in years, too – light-years, where a light-year is just a kind of year. If energy were measured in inverse years or Hz, say, Planck’s constant would be one – with no units. Then, if temperature were measured in inverse seconds (or inverse years), entropy would be dimensionless, which it should be as it is merely a count of items of information – bits, or bytes, or pages. How could temperature be measured like a frequency? One simple way is to designate the frequency at which black-body radiation emits maximally. As we shall see, the frequency corresponding to 6000 K is about 620.7 Hz or, if you prefer, inverse seconds. We leave it as an exercise to show that the temperature is about 1.96 E10 in inverse years. Undoubtedly, these units are inconvenient for most practical purposes, nevertheless the fundamental constants have been over-hyped, have they not?]
In our statement of the First Law as a balance equation we may exclude nuclear reactions or, in case of nuclear reactions where mass is converted to energy or vice versa, we may employ Einstein's famous equation, E = mc2, to equivalence mass and energy. Also, for many applications, we may ignore kinetic energy (not adequate for a rocket in flight) and gravitational potential energy (not adequate for a hydroelectric plant). Under these assumptions the equation is as follows:
The symbol m represents mass. (It’s a variable now not a unit like the meter.) The subscript 2 designates the end of the period under consideration and the subscript 1 indicates the beginning. Thus the expression m2u2 - m1u1 represents the accumulation. (If it be negative, the amount of energy in the control volume has been depleted; i.e., the absolute value of a negative accumulation is a depletion. The subscript i stands for in and the subscript e stands for ex. (Please don't ask why we use Latin prepositions.) Thus the term mihi represents the total enthalpy Hi = mihi for one of the flows entering and the term ĺmihi represents the total enthalpy of all of the flows entering the control volume. (The symbol ĺ represents summation.) Similarly for the term ĺmehe representing all the energy leaving the control volume as a result of material flows including the flow work done on the environment.
The term Qi represents the i-th heat term associated with the transfer of energy into the control volume; the term Qe represents the e-th heat term representing energy leaving the control volume. The term Wi represents work associated with energy entering the control volume; the term We represents energy leaving the control volume. The reader should recognize that both heat and work are phenomena that occur at the boundary of the control volume (the control surface). It doesn't make sense to talk about the heat within the control volume. (However, as in the partitioned control volume discussed above, heat may be transferred from one portion of the control volume to another. Since this transfer is associated with a temperature gradient, one commonly hears engineers and scientists refer to this transfer as a thermal flow or flux. This is fine so long as one realizes that nothing corporeal is flowing.) Heat is the transfer of thermal energy across the control surface unmediated by the flow of material. Associated with each heat term Qi is a temperature Ti , normally the temperature at the control surface. (Notice, we do not say the temperature of the control surface. That wouldn’t make sense as the control surface is incorporeal.) We use the integral calculus when the temperature varies continuously over the portion of the control surface where energy enters. Similarly, for the Qe . Although heat is not associated with the flow of mass, it is accompanied by entropy flow; i.e., it results in a change in the entropy associated with the control volume. Work, on the other hand, is energy transfer that is dissociated from material flow and entropy flow as discussed above. This is not the typical definition of work found in textbooks. Normally, work is defined to be energy crossing the boundary dissociated from mass and capable of raising a weight. Notice it doesn’t say that a weight is raised, but that a weight could have been raised. We don’t like this definition. We are not certain that we can ascertain, in every situation, whether or not a weight could have been raised. We prefer to look at what is rather than what could be. Our approach is not without difficulties however.
Some extremely thoughtful physicists have objected to the depiction of energy and entropy as something, i.e., stuff, that flows. This reminds them of the discredited, long-abandoned theory of caloric, which treats energy as something like water or air, but which is invisible. Anyone familiar with the quantum theory, even a popularization of ideas from quantum theory, knows that we are becoming accustomed to regarding reality as something unimaginably weird and strange. Let us imagine energy as something peculiar too; but, nevertheless, quantifiable and amenable to the ordinary accounting procedures afforded by balance equations – just like water or people. Since energy and entropy are properties of systems, they are relatively well-behaved and have many interesting and useful characteristics.
The Entropy Balance and Lost Work
We are now ready to write the Second Law of Thermodynamics as an entropy balance:
As before, associated with each heat term Qi accounting for energy and entropy entering the control volume is a temperature Ti normally the temperature at the control surface. Similarly, the subscript e refers to heat accounting for energy and entropy leaving the control volume (CV). If the temperature be not constant, we employ the integral calculus. The symbol To represents the temperature of the surroundings of the CV – assumed to be constant. Normally, this is the temperature of the air or a convenient body of water. In most engineering calculations, we will not make a significant error if we take TO to be 288 Kelvin (written 288 K – without a degree sign) everywhere on the Earth both summer and winter. (Temperature in Kelvin is degrees Celsius (Centigrade) plus about 273.16.) Eventually, we shall be comparing the temperature of the Earth to the temperature of the Sun and what might seem to be extreme differences in temperatures if one had to subject one's body to them will be insignificant mathematically. Therefore, we shall assume that the temperature of the Earth is constant at 288 K. However, when the CV is the entire Earth and a shell surrounding it 100 miles thick, the temperature of the surroundings must be considered carefully. The expression L stands for (thermodynamic) lost work, which is really a very suggestive term. We shall see exactly what it represents in the next section on the First and Second Laws Combined. For now, it is what makes the Second Law an equation rather than an inequality. For that reason alone, it is an extremely important concept.
Just as in the case of the First Law the expression m2s2 - m1s1 represents the accumulation term. The two terms with summation signs represent entropy crossing the control surface (in and out, respectively). The terms misi and mese represent mass crossing the control surface each unit of which carries its own specific entropy, whereas the heat terms (ratios of heat to temperature) represent entropy crossing the boundary that is not associated with mass. Notice, as mentioned earlier, the entropy balance has no work terms. (Why?) In this balance equation (unlike the First Law) we have a creation term, namely, LCV / TO. Since Lcv is always positive and To is always positive, this term always represents creation of entropy. It is this term LCV / TO that represents irreversibilities, I, in the process, i.e., I = LCV / TO. Examples of irreversibilities are friction, turbulence (in fluids), the mixing of pure substances, the unrestrained expansion of a gas, and transfer of heat over a finite temperature difference.
Thus, the heat terms, QCS / TCS, in this version of the Second Law must represent reversible heat transfer, i.e., thermal energy that is exchanged infinitely slowly with a thermal reservoir. Considerations of reversibility (approachable but not obtainable by real processes), and irreversibility are of paramount importance in classical thermodynamics – as we shall see.
Definition (Thermal reservoir). A thermal reservoir is a large thermal energy sink or thermal energy source that (i) is capable of exchanging essentially infinite thermal energy without changing temperature, i.e., is very large – like the entire atmosphere, and that (ii) differs in temperature only infinitesimally from the temperature at the control surface, TCS , in the denominator of these terms. (We have employed the subscript cs when the direction of transfer isn’t important.) That is, thermal energy can be exchanged reversibly from a thermal reservoir at Ti + dTi to a control surface at Ti. Likewise, from a control surface at Te to a thermal reservoir at Te - dTe .
The classical example of irreversibility given in popular
expositions is a glass falling from a table to the floor and breaking into a
thousand pieces. (This is like mechanical lost work, 
where
T is the temperature of the system and I is the irreversibility produced in the
control volume. If we subtract the work required to clean up the mess of
the broken glass (and the spilled wine, perhaps) from the mechanical lost work,
that is analogous to the thermodynamic lost work that we are
using in our version of the famous equation; i.e., Lthermo = LCV
= To´I.) We do
not expect to see this process reverse itself spontaneously unless someone is
running a motion picture backwards. In fact that's how we know the motion
picture is running backwards and it makes us laugh (or smile). This
irreversibility of nearly all real processes is referred to as “the arrow of
time” and we all believe in it (or we wouldn't smile at the motion picture
running backward). Thus, at least in this part of the universe and during
this era in the development of the universe, the Second Law tells us that the
entropy of the universe is always increasing. This does not mean, of
course, that the entropy of every control volume is increasing; but, if it's
decreasing in one control volume, it's increasing even faster somewhere
else. We shall consider the important concept of a Carnot engine next.
Figure I-2. The temperature-entropy (S vs T) diagram for a Carnot engine
The thermodynamic cycle for an imaginary Carnot engine is pictured on an entropy-temperature diagram in Fig. I-2. The numbers in circles refer to the following process steps: (1) an isentropic (constant entropy) pumping of the imaginary working fluid (presumably a liquid) from a low-pressure, low-temperature state to a high-temperature, high-pressure state, (2) reversible heat exchange over an infinitesimal temperature difference from a high-temperature heat reservoir to the working fluid, which stays at constant temperature (presumably while the working fluid is changing from a liquid to a vapor), (3) an isentropic expansion of the fluid (presumably through a gas turbine, which delivers work, some of which is used in Step 1) from a high-temperature, high-pressure state to a low-pressure, low-temperature state, and (4) reversible heat exchange over an infinitesimal temperature difference at a constant low temperature (presumably while the working fluid is condensing from a vapor to a liquid). The entire area within the shaded rectangles represents the heat exchanged at the high temperature; the lightly shaded rectangle represents the heat exchanged with the surroundings at the low temperature; the heavily shaded rectangle represents the work done by the imaginary heat engine, i.e., the difference between the heat in and the heat out.
Such a heat engine, operating in such a cycle, is called a Carnot engine, after Nicolas Leonard Sadi Carnot, a French physicist who was born in 1796 and died (young) in 1832. Clearly, a heat exchanger that exchanges heat through an infinitesimal temperature difference would have to have an infinite area, which is inconvenient for purposes of construction. Also, it is difficult to imagine what sort of fluid could go from low temperature to high temperature while being pumped as a liquid (this would be necessary to minimize the portion of work that would have to be drawn from the turbine to operate the device that brings the fluid from low pressure to high pressure). Nevertheless, the Carnot engine is a useful concept that represents an upper bound on efficiency for real heat engines. If someone tries to sell you a heat engine for which an efficiency better than the efficiency of a Carnot engine is claimed, “stay not on the order of your leaving, but depart immediately.” – William Burroughs in Naked Lunch. In the book by P.W. Atkins [3] a much more credible Carnot cycle is illustrated. Any reversible cyclic engine can be a Carnot engine provided only that it has two isentropic processes and two isothermal processes. Atkins illustrates his Carnot engine with a pressure-volume diagram – the well-known indicator diagram employed by James Watt.
The formula for the work from a Carnot engine is easily derived from the Second Law for a cyclic reversible process with no material entering or leaving the system. Remember that, during one cycle of a cyclic process, the system is returned to the state from which it started. Therefore, the accumulation term must be zero. Also, for a reversible process, the lost work term is zero. Thus,
.
To analyze this process denote the change in entropy of the
system during Step 2 as the positive quantity DS . This is precisely equal to the positive change in
entropy of the surroundings during Step 4, as is clear from Fig. I-2. The
system gains entropy during the heat input step and loses the same amount of
entropy during the heat rejection step, which results in no change over the
course of one cycle consisting of all four steps. The heat associated
with energy added at the high temperature (H is for high) is 
,
while the heat associated with energy rejected at the low temperature (L is for
low) is 
. The work done by the
engine, then, is Wrev = 
, while the efficiency, 
Frequently, TL = To and TH is just plain T, so
.
The efficiency of a Carnot engine can be approached as closely as we are willing to pay for, but it can never be attained by a real engine.
The First Law and Second Law Combined: The Two Availability Functions
We now wish to do some simple algebra to get the First and Second Laws Combined. Multiply Eq. I-2 by To to get
Subtract Eq. I-3 from Eq. I-1 to get
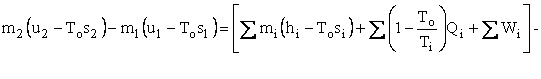
Represent u - Tos by a and h - Tos by b . We now have our availability balance.
[Note in proof (9--9-97). We should refer to a as the Helmholtz availability function and b as the Gibbs availability function, two point functions, like energy, enthalpy, and entropy, that are thermodynamic properties of a simple homogeneous substance. These functions are employed in lost work analysis, the methodology employed here. Exergy analysis is a competing or complementary methodology (depending upon one’s viewpoint) that employs, instead, the thermodynamic property exergy, which, to make matters more confusing, is sometimes referred to as availability. (In the case of the 500 K hot water, used as an example in Chapter 2, the exergy is equal to the availability.) Exergy is essentially the difference between the availability function of the system and the availability function of the same atomic species when they are in mechanical, thermal, and chemical equilibrium with the surroundings. In this essay, we sometimes refer to the availability function as just the availability, likewise for the availability function balance, but we do not employ exergy analysis to such an extent that confusion could arise. When we use the term availability alone, we always mean the availability function
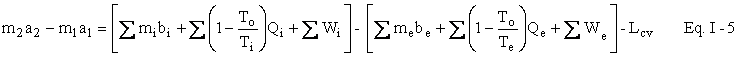
or, in rate form:
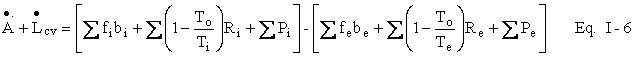
where A = m<a>, mass times average availability,
i.e., availability per kilogram. When we wish to denote rate of accumulation
of availability, say, per unit time, we merely place a dot over the symbol for
availability. This is standard practice among physicists and engineers
and applies to anything; i.e., if X stand for volume of beer drunk, 
(spoken
and sometimes written ‘X dot’) stands for the volume of beer drunk per unit
time at a particular time of interest or over a period of time such that the
rate of guzzling remained constant. Although averages are denoted
normally by angular brackets, viz.,
we may omit the brackets when no confusion can arise, in which case X dot stands for the average rate of guzzling during the period of interest. (Aren’t you glad you decided to read this?) But, we haven’t said what kind of availability function we are talking about and, in keeping with Murphy’s 352d Law, there are two kinds (represented by a and b).
Amazingly, despite the incredible importance of the quantities a and b, they do not have decent names even. Perhaps, this is indicative of a less than felicitous point of view adopted by scientists and engineers over the years. To assist our memories, let us call a = u - Tos the Helmholtz availability function (since u - Ts is the well-known Helmholtz function) and b = h - Tos the Gibbs availability function (since h - Ts is the well-known Gibbs function).
Figure I-3. Diagram to illustrate lost work
In rate equations, we find it confusing to employ derivative notation. If mcs is the quantity of mass crossing the control surface, we shall refer to the rate at which mass crosses the control surface as fcs (for flow). Similarly, Rcs is the rate of heat transfer across the control surface, and Pcs (for power) is the rate at which work is done on or by the control volume. These have convenient mathematical equivalents, which you may know already or will learn later.
We may employ Eq. I-6 to familiarize ourselves with important
thermodynamic concepts. In particular, let us consider a closed system in
steady state. The accumulation term, 
, is zero and the
entrance and exit terms, ĺribi
and ĺrebe, are
both zero. Suppose, in addition, that no work is done on or by the
control volume. Eq. I-6 is reduced to
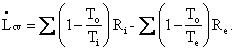
Let us select a concrete example to see how this equation makes clear the meaning of lost work. Suppose we have a long metal rod – well-insulated except for the ends – touching a practically infinite high-temperature source like a large boiler at temperature Th at one end (of the rod) and the atmosphere or ground at temperature To at the other as shown in Fig. I-3. The control surface is taken to be the outside of the insulation and the bare metallic ends of the rod. The heat influx rate is Ri = RH, whilst the heat efferent rate is Re = RL = Ro. The insulation is important because, under these conditions, the heat out term Re will be multiplied by 1 – To/To = 0 , which would not be the case if heat leaked out the sides at higher temperatures. To maintain steady state, we must have a positive heat term, RH = Ri, entering the control volume from the boiler at temperature Th. Then the lost work is easily seen to be precisely the work that would have been done by a reversible (Carnot) engine operating between a heat source at temperature Th and rejecting heat to a heat sink at temperature To.
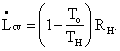
[This term 1- To/TX occurs so often that we find it expedient to further simplify our equations by denoting it CX (for Carnot). The above equation could have been written
which is perhaps going too far.] Thus, L really does represent the work we could have gotten from an ideal process but didn't get from our real process, which wasted the high-temperature heat that was added to it. Question: Where was the irreversibility in this system?
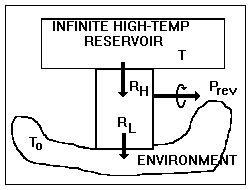
Figure I-4. A completely reversible device
In a reversible steady-state process
conducted upon a closed system, a heat engine, say, that produces work,
heat enters at temperature 
and leaves at temperature To
, in which case Eq. I-6 reduces to
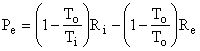
since the accumulation term, A dot, equals zero (steady state), the terms representing mass entering and leaving are zero (closed system), and the lost work term, Lcv dot, equals zero (reversibility). The work done by the control volume is equal to the reversible work, i.e., the maximum amount of work that can be extracted from Ri at temperature Ti. Thus,
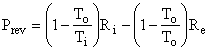
as shown in Fig. I-4. But, the second term in parentheses is identically zero, therefore the equation reduces to
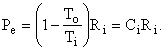
Thus, the control volume is a heat engine with an efficiency h = We / Qi = 1 - To / Ti = Ci. This is precisely the efficiency of a Carnot engine. We know that no device can have an efficiency as high as that of a Carnot engine except a Carnot engine itself; therefore, our control volume must be a Carnot engine, the imaginary device, discussed above, whose efficiency can be approached but never attained.
Finally, let us consider a reversible steady-state process with one stream entering and one stream leaving. We wish to know the maximum amount of work that could be obtained from such a process. This serves as an upper bound on the work that we can expect to obtain from a process with this input and this output.
Prev = fibi - febe .
Let us put these concepts to use immediately.
Overall Availability Analysis of Earth
Note (10-7-05). This section serves no useful function within the context of this essay, therefore it has been withdrawn. At some future time, it will be presented as an ancillary essay hyperlinked on my website.
Note (4-11-07). Lately I have revisited the calculation and computed the value of the maximum amount of reversible work that can be performed on Earth on a completely different basis, namely, that the control volume is a ball concentric with the Earth with a radius 100 miles greater so as to include the atmosphere. The effective temperature of the surroundings is taken to be the temperature of deep space. I am adding the calculation here as a point of interest:
Helmholtz availability is U – ToS = A and Gibbs availability is H – ToS = B; therefore, the availability balance, which is obtained by multiplying the entropy balance equation by To and subtracting it from the energy balance equation, is as follows:
where U is internal energy, H = U + PV is enthalpy, W is work, Q is heat, and T is temperature. The subscripts i, e, and o refer to in, out, and environment. The enthalpy of an ensemble of photons is four-thirds of its energy. The effective temperature of the sun was computed to be 5760K and the effective temperature of Earth was computed to be 254K. Earlier work on the availability balance around Earth can be found at http://dematerialism.net/Earth Part 1.html and http://dematerialism.net/Earth Part 2.html.
The correct input and output terms to the Earth’s control volume are the enthalpy in and the enthalpy out. The Gibbs free energy of photons and elements is zero; so, Hi = TiSi and He = TeSe. Also, since the Earth is approximately in energy balance regardless of global warming, Hi = He = H. Equation 3 for the maximum reversible work for the Earth’s steady-state control volume reduces to:
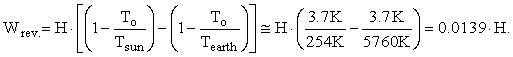
This gives a value for the maximum reversible work of 0.0139 · 1.33333 · 127,000 TW = 2358 TW. This is a very large amount of reversible work, but much smaller than the 183,533 TW I computed when I assumed that the energy from the sun was discharged to the coldest temperature on Earth.
Global Warming?
Introduction
Will the burning of fossil fuels cause global warming? Computer experiments seem to indicate that, all things being equal (and they never are), an increase in the carbon dioxide (CO2) concentration in the atmosphere will allow more infrared radiation to be trapped within the Earth's atmosphere and cause the average global temperature to rise slightly (one or two degrees Celsius) over a number of decades. This would lead to some melting at the polar ice caps and many coastal cities would be under water. Other undesirable effects might occur – as well as a few desirable effects. No one knows for certain what will happen – in particular because about half of the carbon dioxide that goes into the atmosphere is unaccounted for. Freeman Dyson, in a recent lecture at Rice University, suggested that the biosphere might become so “hooked” on CO2 that we would eventually have to burn limestone! Of course, he was only joking, but one never knows!
Be that as it may, we have certainly released a great deal of carbon dioxide to the atmosphere during the last fifty years that had been withdrawn from the atmosphere by photosynthesis over extremely long periods of time. Moreover, Keeling et al. [see p. 319 Häfele [4]] measured the concentration of CO2 at Mauna Loa in Hawaii over about thirty years and found an increase in the yearly average (it goes through a yearly cycle) from about 315 parts per million (ppm) to well over 700 ppm. Therefore, it makes sense to analyze how we might have to alter our use of fossil fuels if global warming were a genuine threat.
Example of Burning Methane and Octane
If we rearrange Eq. I-6 for the steady-state (
= 0),
adiabatic (no heat term), reversible (no lost-work term) combustion of methane,
say, we can write
The control volume for this thought experiment is pictured in Fig. I-6. Moreover, if we set T = 300 K , then the Gibbs availability function is equal to the plain Gibbs free energy, g = h - Ts, which we can look up in a handbook [12] and
On the basis of one gram mole (9) of methane, we compute, corresponding to the chemical equation,
Wrev = gmethane+ 2 goxygen - [gcarbon dioxide + 2gwater] =
= [-12.14 + 0.00] - [-94.26 + 2 (-54.64)] = 191.4 kcal per gmole methane.
Figure I-6. Control volume for reversible, adiabatic combustion of methane
(The free energy of oxygen is zero because the free energies of all elements are zero. The non-zero Gibbs availabilities are the same as the Gibbs free energies or the free energies of formation since T = To and they can be found in Table 3-202 pp. 3-137 to 3-144 in the Chemical Engineers’ Handbook [12].) (Also, I find it less confusing to enter negative quantities as such and use parentheses appropriately. I recommend that students follow my example and make liberal use of the change-sign button on their calculators.) So far so good, but what happens if, to avoid global climate change, we must dissociate the carbon dioxide to oxygen and carbon (which last species might end up as the now-famous buckyballs [13]) to prevent it from entering the atmosphere?
Oxygen, O2 , and carbon, C , are elements and as such are assigned a Gibbs free energy of zero. Thus, the reversible work that must be supplied to dissociate CO2 is just 94.26 kcal per gram mole of carbon dioxide, the negative of the Gibbs free energy of carbon dioxide, which we know from the previous calculation. But, these figures represent the best we can do under impossible-to-obtain ideal circumstances. Suppose, to be optimistic, we agree that we could carry out the combustion and the dissociation at the amazing efficiency of 70%. (Remember we must count the energy used to make the apparatus and some portion of the energy expenses of the people involved with the process.) In that case, the net work we should obtain by burning fossil fuel without releasing carbon dioxide to the atmosphere would be Wactual = 0.70 ´ 191.4 – (94.26 / 0.7) = -0.68 kcal /gmole methane, i.e., a dead loss. Moreover, methane is the hydrocarbon with the highest possible hydrogen to carbon ratio, therefore we should not expect to do better with any other fossil fuel and the combustion of fossil fuels would be infeasible – under this scenario. (The reader realizes that we are oxidizing the hydrogen in methane to add water to the environment, which is OK, but we are not oxidizing the carbon, which is OK (less oxygen is consumed), and producing pure carbon, which may or may not be OK.) I suppose that the carbon dioxide could be eliminated from the flue gases with less expenditure of energy than we have computed – perhaps by a new technology that produces something useful – maybe a building material; but, as we shall make abundantly clear, we have many additional compelling reasons not to depend on fossil fuel. (It has been suggested that energy could be obtained by reacting fossil fuels in such a way that carbon dioxide is not produced. Reactions where the carbon ends up in useful organic compounds all turn out to be net consumers of reversible work according to my calculations with limited data, but who knows?)
Rather than bore you with a similar calculation for octane (a fuel that behaves much like the much-more-complicated mixture we call gasoline) let me provide you with the Gibbs free energy of octane, namely, g octane = 4.14 kcal /gmole, and leave it as an exercise to show that the break-even efficiency for burning octane and dissociating the carbon dioxide in the flue gas is approximately 77.7%. The formula for octane is C8H18. A passing familiarity with general chemistry is necessary to work this exercise.
Of Things Not Treated
In this brief introduction to thermodynamics, we avoided power cycles other than the imaginary Carnot cycle. Also, in a course in a chemical engineering department, a large chunk of time will be devoted to vapor-liquid equilibrium. This is the most difficult scientific information to obtain when designing sensitive separation processes. (One of the authors has seen with his own eyes a book of such data produced from photocopies and not exceeding 300 pages by much if any that was for sale at the time for $2,500 and sales were satisfactory. Normally, liquid-liquid equilibrium is treated too but not in quite so much depth. Many thermodynamics textbooks analyze mechanical and chemical equipment from pumps to reactors. This is way too nuts-and-boltsy for us. Finally, thermodynamics is the key to chemical reaction equilibria and, normally, a chapter is devoted to chemical reactions. In mechanical engineering departments, flow through turbines and nozzles, including supersonic flow and shock waves, is studied. Theoretical chemists and physicists seem to pay more attention to the fundamental mathematical relations and special relations among the distinguished partial derivatives derived from them. I believe I made in clear that the Second Law can be studied from the viewpoint of impossible processes, namely, the Clausius Statement of the Second Law and the Kelvin-Planck Statement. We don’t bother with these at all; balance equations are so much more useful.
March 15, 1993
Revised October 13, 1997
References
1. Truesdell, Clifford, “Some Challenges Offered to Analysis by Rational Thermomechanics”, in Contemporary Developments in Continuum Mechanics and Partial Differential Equations, Eds. G. M. de La Penha and L. A. J. Medeiros, North-Holland (1978).
2. Van Wylen, Gordon J. and Richard E. Sonntag, Fundamentals of Classical Thermodynamics, John Wiley and Sons, New York (1978).
3. Atkins, P.W., The Second Law, Scientific American Library, W.H. Freeman, New York (1984).
4. Häfele, Wolf, Editor, Energy in a Finite World, Ballinger, Cambridge, MA (1981).
5. Yourgrau, Wolfgang, Alwyn van der Merwe, and Gough Raw, Treatise on Irreversible and Statistical Thermodynamics, Dover, New York (1982).
6. Hammond Headline World Atlas, Hammond, Maplewood, N.J. (1986).
7. Gegani, Meir H., Astronomy Made Simple, Doubleday and Co., Inc., Garden City, N.Y. (1955).
8. Wayburn, Thomas L., “On Space Travel and Research”, in The Collected Papers of Thomas Wayburn, Vol. II, American Policy Inst., Houston (Work in progress 1997).
9. Gleick, James, Chaos: Making a New Science, Viking, New York (1987).
10. De Nevers, Noel and J. D. Seader, “Mechanical Lost Work, Thermodynamic Lost Work, and Thermodynamic Efficiencies of Processes”, Lat. am. j. heat mass transf., 8, 77-105 (1984).
11. Szargut, Jan, David R. Morris, and Frank R. Steward, Exergy Analysis of Thermal, Chemical, and Metallurgical Processes, Springer-Verlag, New York (1988).
12. Perry’s Chemical Engineers’ Handbook, 6th Edition, Large staff of specialists, McGraw-Hill, New York (1984).
13. Kroto, H. W., J. R. Heath, S. C. O’Brien, R. F. Curl, and R. E. Smalley, “C60: Buckminsterfullerene”, Nature, 318, pp162-163 (1985).