Overall Availability Analysis of Earth, Part 1
Table of Contents to Part 1
Why Bother? The Technical Usefulness of the Calculation is Minimal.
Computing the Lost Work or Maximum Reversible Work for Earth’s Control Volume
Introduction
Dave Bowman’s Disclaimer
Prof. Bowman may wish to distance himself from some of the definitions, logic, conclusions, and other statements rendered in this appendix. This section is where that should be done – unless, of course, he objects, also, to that arrangement, in which case whatever must be done will be done. Also, Dave, at some time you should come to realize how politically radical this book really is. You may find that you are (i) too conservative or (ii) justifiably concerned about your association with an extremely radical book.
In addition, Dave and I share a difference between his view that a photon gas is not a simple compressible substance and that it does not do injection work upon the control volume and my view, which I have not expressed previously in the following manner: It seems to me that radiation fits into the framework of thermodynamics a little differently than do other manifestations. It is as though a photon carries the temperature of the Sun into the control volume until it strikes an ion, atom, or molecule, at which time it does transfer momentum to that particle and, therefore, it does do injection work to allow something within the control volume, like a tree leaf or a generic solar collector, to be an agent for the performance of useful work subsequently. We both agree that nothing happens until the photon strikes something. Enthalpy is defined to be the internal energy plus the injection work, therefore we both agree that it is the enthalpy that should be computed.
The Control Volume
We wish to make an availability balance over the entire Earth including its atmosphere but excluding its core. The exterior component of the control surface (CS) is taken to be a sphere 100 miles from the average level of the sea at the equator, which describes it more accurately than is justified by the precision of our numerical techniques. The interior of the Earth is excluded from our control volume, since, for all practical purposes, we cannot get to it unless it chooses to come to us. The control volume (CV) for this analysis is shown as the shaded region in Fig. I-5 on the next page. The thin shell (of Earth) outside the core is supposed to contain every agency of useful work - from the roots of trees to heat engines at the bottom of the deepest mine or well.
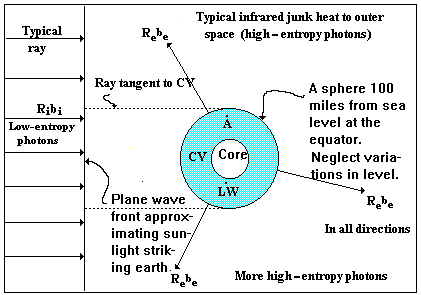
Figure I-1. Control volume for the calculation of availability accumulation on Earth due to sunlight
Imagine for a moment the Earth divided into two hemispheres by a plane parallel to the plane wave front of the incoming radiation from the Sun. At every instant in time, the hemisphere facing the Sun is accepting radiation at 6000K. In our thought experiment this will be used to do reversible work inside the control volume, therefore an imaginary heat engine will reject heat to the surroundings at 300K, which we may take to be the Earth and such thermal reservoirs as we may take advantage of such as oceans, lakes, and rivers, which, in this analysis, are imagined not to contribute further to the reversible work. Simultaneously and roughly at the same instantaneous rate that the hot hemisphere is receiving energy from the Sun, the dark hemisphere is radiating energy from the 300K thermal reservoirs, represented by the Earth’s core in Fig. I-5, to deep space, the effective temperature of which is approximately 4K. It is difficult to imagine how a reversible heat engine could be constructed to accept heat at 300K and reject heat at 4K; nevertheless, we should consider the availability associated with this radiant heat transfer.
Since the Earth rotates, the entire control volume of Fig. I-5 should be considered twice: first, with the temperature of the surroundings, namely, the thermal reservoirs, equal to 300K, and, second, with the temperature of the surroundings, namely, deep space, equal to 4K. The two calculations are imagined to be superposed upon one another and to take place simultaneously. In the sequel we shall neglect the second calculation.
Why Bother? The Technical Usefulness of the Calculation is Minimal.
We already know that the Helmholtz availability budget provided by Mother Nature is virtually astronomical. Since this might encourage people to embrace “The Myth of the Infinite Earth”, why should we go to so much trouble to provide an estimate of a number that, quite frankly, is useless for further computation or analysis?
The possibility of achieving a sustainable, one-kilowatt-per-capita, soft-energy society can be estimated with greater confidence by comparing the 10 TW that we hope to harvest from biomass to the world photosynthesis rate of about 100 terawatts [4] than by comparing human needs to the Earth’s ~150,000-terawatt total power throughput because of the numerically intractable disparity in scale between human needs and the total figure and the difficulty of computing Mother Nature’s availability budget for running the weather and other natural phenomena that make the Earth habitable. (For reasons known only to Herself, Mother Nature seems committed to making the Earth a home for living things.)
If we could harvest 10% of the 100 TW stored (continuously) in the biosphere by photosynthesis without doing major ecological damage in a world such that the population had stabilized at ten billion ‘souls’ – to be as optimistic as we can be, we could enjoy a one-kilowatt-per-capita economy that (for intelligent creatures) should be sufficient to live well in harmony with Nature. One kilowatt per capita is more than thrice Bangladeshi consumption.
The
lost power term in the Combined First and Second Law Availability
Balance around Earth represents the maximum rate at which work can be
done
inside the Earth’s control volume. Despite the lack
of technological
usefulness, we have three reasons to compute an estimate of the lost
power term
in
Eq. I-7, the First and Second Laws Combined:
=
.
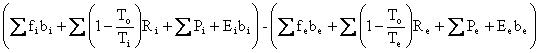Eq. (I-7)
First
and foremost, we said we would put the Combined First and Second Laws
to use
immediately and this is a grand use indeed. So, we have done
this to show that
it can be done. Second, when 
, the value of represents a hard limit on human activity
in a
sustainable society, which proves the finiteness of such a
limit. And, third,
good scholars do not suppress relevant information uncovered during
their
research. Every true scientist would prefer to report that
his theory is false
or to report “no results” than to report an
instance of an experiment that
proceeded according to the predictions of his theory. A true
scientist should
be his own most severe critic. Frequently, we learn more from
falsifications
than from corroborations of our conjectures.
For example, we know that the upper bound we are computing is astronomical and is likely to persuade those who are vulnerable to unjustified optimism that human society has more than enough sustainable high-grade ‘energy’. These are people who, like ourselves, have no idea of the recovery costs (both direct and indirect) for any type of sustainable energy – firewood excepted. Moreover, they have no idea how much energy is likely to be consumed by turbulence in the air of the atmosphere and the water of the seas. They have not studied the energetics or the effects upon various living things of the shifting of the tectonic plates, volcanism, forest fires, storms, earthquakes, El Niño, the Gulf Stream, normal circulation of oxygen, nitrogen, carbon dioxide, water, and other elements that consume availability on a periodic basis, and catastrophic weather in the sense of sudden –discontinuous – changes. In short, they don’t know if 150,000 terawatts (150,000,000,000,000,000 watts) is a large amount of availability or a small amount of availability on a global basis – anymore than we do. We, at least, are trying to assess the likelihood of scarcity or abundance beginning with scientific methods, which we shall employ until they fail and must be abandoned – probably in favor of prudence.
Acknowledgments
Dan Wilkins, an astronomer at the University of Nebraska, introduced Wayburn to Dave Bowman, a physicist at Georgetown College, who has provided nearly every theoretical idea worth considering in this attempt to get an availability balance around the entire Earth. This section is dedicated to Dan Wilkins, a gentleman and a scholar. Others whose help should be acknowledged are Jim Green, John Mallinckrodt, Leigh Palmer, and Brian Whatcott. These are Internet friends. Gentlemen, we thank you all.
Nomenclature
Note (10-13-97)
In the Bowman calculation of lost work inside the Earth’s CV at steady state, a number of standard constants, such as the radius of the Earth, were employed. Wayburn has changed these to the data that appear in the references on his shelves. This has almost no effect on the answers obtained. Also, Dr. Wayburn derived all of Prof. Bowman’s equations and computed essentially the same values as did he. The creative leaps, however, were due to Bowman. Bowman calculated the solar constant by applying the ratio of the Sun’s surface area to the surface area of a sphere centered at the Sun with the Earth on its surface, i.e., by the inverse square law. Wayburn took his solar constant from Häfele [4]. We shall use Bowman’s calculated Ksolar to harmonize with the numbers from which he calculated it. We shall employ Wayburn’s standard data (except for Ksolar) without mentioning the minor differences.
Constants and Variables
a , the Earth’s albedo, the fraction of power, Pasun,in, that is immediately reflected and, for practical purposes, has no effect on our CV. We computed the value a = 0.3 from Fig. 2-9 in Chapter 2, which was taken from Häfele [4].
h , Plank’s constant, 6. 626 ∙ 10-34 J sec [5, p. xviii].
k , Boltzmann’s constant, 1. 380 ∙ 10-23 J / K [5, p. xviii].
r = TCV / Tsun , the ratio of the effective temperature of the far-infrared radiation from the Earth to the effective temperature of the (nearly) blackbody radiation from the Sun.
rCV, radius of Earth at equator plus 100 miles = 6,539,000 meters [6].
rearth, radius of Earth at equator = 6,378,000 meters [6 (back cover)].
rearth,avg, average of equatorial and polar radii = 6,367,500 meters [6 (back cover)].
rsun,
radius of Sun = 
meters [7, p. 116].
Aproj,e, projected area of Earth as seen by plane wave from Sun = 127.4 ∙ 1012 m2.
Aproj,cv, projected area of Earth’s CV as seen by plane wave from Sun = 134.3 ∙ 1012 m2.
Asphere,e, area of Earth’s spherical surface = 509.6 ∙ 1012 m2.
Asphere,cv, area of outer surface of our CV = 537.3 ∙ 1012 m2.
D , average distance between the Sun and the Earth = 1497 ∙ 108 meters [7, p. 116].
Ksolar or Ks, solar constant (calculated by Bowman as Stephan-Boltzmann flux times inverse square ratio, ψ) implies that Ks = 1350.7 W/m2, but looked up by Wayburn in Häfele [4, p. 151], which offers 1353 W/m2. In this computation we use Bowman’s number.
Rb[T], radiant energy flux or rate of radiant energy flow per unit area from a blackbody. This is determined by the Stephan-Boltzmann Equation:
Tsun, effective temperature of Sun’s surface as a blackbody radiator, 5760 K [4, p. 151] .
Tearth,surf, average temperature at surface of Earth, 288 K .
Tcv,IR rad or, to save typing, Tcv, effective black body temperature for radiation of far-infrared (IR) junk heat from Earth’s CV, 254 K was computed from energy balance.
T0, the thermodynamic ‘temperature of the surroundings’, which we take equal to Tearth,surf = 288 K.
εcv, emissivity of the Earth’s control surface, one minus the albedo
εIR, average emissivity of the Earth’s outgoing far-infrared (far-IR) waste flux. The Earth is well approximated as a blackbody regarding its outgoing IR flux, so we use εIR = 1.0 .
εsun = 1.0 as the Sun is normally treated as a blackbody whose effective temperature is 5760 K.
η, Carnot efficiency
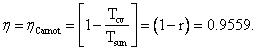
ξinv. sq., inverse square law for surface of Earth to top of atmosphere
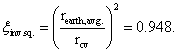
σ, the Stephan-Boltzmann constant
where
.
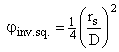Notice
that the 1/4 is already included in this variable. 
.
Ψinv.sq., inverse square law for surface of Sun to Earth
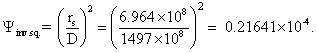
Φemit,earth = εIR∙σTcv4 = 236 W/m2, the average far-infrared flux emitted from the Earth’s upper atmosphere. (The straightforward calculation from an Earth’s surface at 288 K gives a disappointing 390.1 W/m2 . Even applying the inverse square law to the datum reduces it to 369.9 W/m2 only. It is fair to say, though, that much of the radiation emitted from the Earth does not come from the surface.)
Φabs,earth =
¼∙(1-a) ∙Ksolar
= 236 W/m2,
the average solar
flux crossing the Earth’s outer control surface.
(The use of Häfele’s [4]
choice of 
=
1353 W/m2 rounds
off to 
since
the data used to compute 254 K is that which gives a solar constant of
1301.7
W/m2,
which
is the value we shall use throughout this paper – making
changes wherever
necessary.)
Photons and Only Photons
To
write the Combined First and Second Law over the Earth’s CV
showing
the radiation terms, the rates 
(resp.) in photons per
second
at which photons enter and leave (resp.) the CV could be computed and
multiplied by the corresponding average value of the ratio of the mean
total
enthalpy (in joules) divided by the mean total number of photons and
the
constant value of the ratio of mean total entropy (in joules per
Kelvin)
divided by the mean total number of photons. Photons do not
have mass per
se, but they do carry pressure, p,
internal energy, u,
enthalpy, h,
and entropy, s.
Also, photons have a Gibbs availability function, b, which
would be zero for a photon gas whose (constant)
temperature happened to be 
.
That is, in
the case of T = ,
the Gibbs availability
function equals the Gibbs free energy, which is zero for a photon
gas. Thus,
we might do well to remember that H = TS for
photons. Alternatively, we can
compute the thermal power in and out, the enthalpies, and the entropies
for the
entire ensemble in one piece. We do both.
Many
readers may be surprised to learn that a photon gas is a simple
compressible substance that behaves like an ideal
or perfect gas. As in ideal gases,
photons do not interact with
each other. They interact with atoms, molecules, and other
objects, but not with
each other [5]. A photon gas, as an example of what is known
in statistical
mechanics as a partially degenerate Bose-Einstein gas, does not have an
equation of state like p = 
(T,V) with two independent
variables. But rather, p = 
, which is not a legitimate
equation of state since pressure is a function of one variable
only. The
densities for every thermodynamic property can be written as functions
solely
of T. For example, the energy density of a photon gas in
equilibrium with the
walls of a black body cavity that contains it is 
= 
= 
, where 
is a special
symbol used (in this appendix only) to notify the reader that the
object within
the primary parentheses is a density.
If j(U(T)) is energy flux from the photosphere of the Sun to the Earth, where
one can write down a generic formula for the total influx rate of Property X to the Earth’s CV in terms of the flux of X leaving the photosphere of the Sun or the density of X in the photosphere (of the Sun):
This is the solar constant, Ksolar or Ks = 1350.7 W/m2 calculated by Bowman. It is the number we use in these calculations.
[The identifier j is not expected to indicate a flux outside of this appendix; however, some of us use it in e-mail because of its typographical feasibility. For example the flux of entropy from the Earth might be written j_e (S, cv) = 4/3*sigma*T(cv)^3, where the under-bar ( _ ) is used to indicate subscript and the caret ( ^ ) indicates exponents (as in BASIC.) This is not quite standard notation. Perhaps, e-mail typography will become barely adequate soon.]
The
Stephan-Boltzmann equation permits us to compute the flux of
photons irradiated from what is known as a black body as a function of
the
temperature alone. Without going into details, we shall
present this
fundamental and important equation in a primitive form that employs a
constant
called 
(simply
a
in Yourgrau et al. [7], however
we have used a
for albedo) but
from which the Stephan-Boltzmann equation, in its normal form, can be
derived
easily. 
is
the energy flux or rate of radiant energy flow per unit area from a
black body
– hence the subscript b.
A black
body is a perfect emitter as well as a perfect radiator. is a function only
of the (equilibrium) temperature of the radiating black body.
It is easy to
show that
Eq.
(I-8)
where
k
is Boltzmann’s constant, h is
Plank’s constant, and c is the
speed of light. Far from a
fundamental constant of the universe, k
is precisely the ideal gas constant divided by Avogadro’s
number. Boltzmann’s
constant is 
. Plank’s
constant is 
. In the
cavity of a blackbody at 5760 K = Tsun,
which is surprisingly well-approximated by the
photosphere of the Sun, we have for the photon density
and for the photon flux
where
and
In a little ‘disquisition’, distributed over a physics ‘list server’, Dr. Bowman has shown that most of the so-called ‘fundamental constants of the universe’ are no better than conversion factors. If energy were measured in inverse seconds, Plank’s constant would be one – with no units! If energy were measured in Kelvin, entropy would be dimensionless, which, as an accounting for the amount of information deficiency, it should be! The speed of light in vacuum, c, is 3.0∙108 meters /sec . It is really a conversion factor between time and length, both of which should be called interval from special relativity. If we measured time in years and distance in light-years, the speed of light would be one and length could be measured in years, which might be slightly inconvenient in nano-technology. Finally, the Stephan-Boltzmann constant is 5.6697∙10-8 J∙m-2∙sec-1∙K-4. Equation I-8 is a very important equation; however, it applies only to photons in equilibrium with a black body from which they are radiating, e.g., the inner walls of a blackbody cavity.
The literature provides us with many useful formulas for photon gases. The difficulty comes in deciding if the photons are in equilibrium with their surroundings in any useful way. In the photosphere surrounding the Sun, the photons behave somewhat as photons in a blackbody cavity in equilibrium with the walls of the cavity.
[Note. But, even though the photosphere is not in equilibrium, its steady-state behavior allows it to act as if it were in equilibrium (except for the turbulence and convective effects induced in the unstable gas because the temperature is greater below – nearer the center of the Sun – than above). Even though the photosphere’s turbulent gases are not equilibrated, the electro-magnetic radiation is much better behaved and acts as if it were in equilibrium. – Dave Bowman (9-3-97)]
We shall treat these photons as blackbody radiation at an effective temperature of 5760 Kelvin. As we shall see, photons obey uniform and simple laws when they travel in rays to the Earth, therefore, they might just as well be in equilibrium with the Sun. The formulas we use give the correct values for thermodynamic properties even though the photons are not truly in equilibrium. The photons behave as though they were in equilibrium, which allows these calculations to be made.
If the photons were emitted with a given S/N ratio in a state of (effective) equilibrium, then, as they propagate through space their entropy does not change (even though their propagation through space is no longer an equilibrium situation). The photons propagate adiabatically through space. The reason for this is that, for the energy, entropy, and number densities, we have:
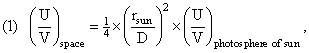
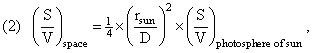
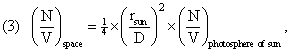
using the above formulas relating ρ(X,space) to ρ(X,sun); and
the usual equilibrium as employed in electromagnetism, thermodynamics, and statistical mechanics; and, therefore,
where Tentering CV = Tsun.
Similarly, for the photon number we have
and, therefore,
Let
Then, let
Notice that the ¼ is already included in this variable φ, which is equal to 0.0541∙10-4. The density of U, S, and N might be represented as ρ(X,space) = φ ∙ ρ(X,photosphere), which transforms densities in the photosphere of the Sun to space – but, especially, to the Earth’s CV. This simple relation is supposed to apply to X = U, S, and N. Presumably, it would apply to H, and the potentials, whether one calls them F and G, or A and B.
The constant value of the ratio of the entropy of any ensemble of photons divided by the number of photons is obtained as follows: We use
the regular formula for getting S from U. This is valid in space, too. Also, for the photon number, we get
;
and, for space, we get
.
Thus,
We see
that the equilibrium relationships among U, S, and N are
preserved for their corresponding fluxes in space because the density
for each
one gets mapped from its equilibrium value in the photosphere to its
outer
space version (out at the Earth's orbit) according to the same
mapping ρ(X,space) = φinv.sq.
∙
ρ(X,photosphere) or ρ(X,space) = 0.0541∙10-4 ∙
ρ(X,photosphere). So we
end up with the result that S/N = 3.602
k for both the
quasi-equilibrium situation in the photosphere and
for the nonequilibrium situation of solar fluxes in outer space.
Computing the Lost Work or Maximum Reversible Work for Earth’s Control Volume
Given
the internal energy, U, the formulas for other properties of
photons are easy to write in terms of U. For example, H = 
, 
, and the
Helmholtz availability function A = U - ToS.
Since, for natural reasons,
the CV can be assumed to be in energy steady state – global
warming
notwithstanding; i.e., 
= 0; and, since To
is taken to be constant
in this rough calculation; and, further, since the assumption
upon which this
exercise is based is a steady-state Earth with respect to Helmholtz
availability; i.e., 
- 
= 0: we may conclude
that the Earth’s CV is in steady state with respect to
entropy as well, that
is, 
.
The value of To, the temperature we should use for the surroundings of the entire Earth, is intended to be the lowest temperature ‘infinite’ heat sink available, usually the atmosphere or a large body of water, whichever we think we can get away with polluting. The heat sink is infinite in the sense that any amount of waste heat we dump into it is too small to change its temperature measurably. Our choice of To corresponds to the nominal temperature of the Earth’s surface, namely, 288 K. We are not likely to be able to do better than that. If one of these space fanatics suggests that we build a heat engine that exhausts to the background temperature 3.7 K of deep space, we should do our best to discourage him for all the reasons mentioned in Wayburn’s essay on space [8].
The
industrial nations of the world have not even begun to consider the
possibility that we ought to stop deficit spending of availability over
every
other priority. I suppose, then, that a steady-state Earth
with respect to
availability is a theoretical idealism. Nevertheless, let us
impose the
condition as
part of our demand for a sustainable society. The possibility
of running an
availability surplus
is
unthinkable just now. Nevertheless, under these restrictions
we shall get a
very rough idea of just how much availability we can spend without
running an
availability deficit.
Let us discuss the First Law and the meaning of some of the terms in it for photons. We shall compute the rate of lost work using a First Law energy balance in connection with additional Second Law concepts.
First Law:
where the rate of change of internal energy of the Earth is
the mass (in kilograms) times the (average) internal energy per kilogram – not per cubic meter. Of the other variables, only the mass flow rate, f; the heat transfer rate, R; the rate at which work crosses the control surface, P; and the photon rate, E, are nonstandard. Therefore, if the quantity of interest is denoted X, the rate at which it enters the Earth’s CV will be Ri(X) and the rate at which it leaves will be Re(X) .
In our
problem, we shall have steady state with respect to energy
within the control volume, which gets rid of the left-hand side . Neither
do we have to consider material flowing into and out of our CV,
therefore the fxhx
can be neglected. Although
radiation is frequently treated as a form of heat transfer (radiant
heat
transfer), we shall not have to treat it as having anything to do with
heat
within our First Law setting, so the Rs go too. We are left
with
where
Therefore,
Before we proceed further, we must take a careful look at the various categories of thermal flux that contribute to the energy balance around the Earth. Of course, we know that energy is not a substance; and, therefore, thermal flux is an abuse of language, but we encourage the reader to take a tolerant view of our cavalier use of metaphor. Also, we shall compute the rate of entry and egress of thermal energy from our control volume. This will require the calculation of the effective temperature of the far-infrared ‘junk heat’ leaving the Earth.
The
solar constant, Ksolar,
is about 1350.7 W/m2 .
That means that where the straight line joining the center of the Sun
to the
center of the Earth crosses the outermost layer of the Earth's
atmosphere, 100
miles above sea level, say (since we wish to calculate an upper
bound on 
), the mean energy
flux due to radiation from the Sun is about 1350.7 Joules per second
per square
meter. The solar constant isn't quite constant, but we shall
use it for very
rough calculations; so, we may safely ignore the variations.
The atmosphere is
a very thin shell surrounding the Earth and whatever we take to be the
outermost layer has a radius less than 100 miles (160,934 meters)
greater than
the (equatorial) radius of the Earth, which we shall take to be
6,378,000
meters. Further, we shall assume that the sunlight strikes
the Earth in a
plane wave. Actually, the Sun is more like a point source in
the sky
subtending just over a half of a degree, but the calculation of the
total
energy entering the Earth's system is simpler if we assume all of the
photons
are traveling in paths parallel to the aforementioned line connecting
the
centers of the two bodies, which gives a value for the total power from
the Sun
entering the Earth's system that is slightly high. (The
Earth's system is all
of the mass contained within a large (concentric) sphere just beyond
the
furthest reaches of the Earth's atmosphere and outside the smaller
(concentric)
sphere representing the depth beneath the Earth's surface that is, for
all
practical purposes, unreachable. It is the CV depicted
symbolically in Fig.
I-5 on p. 144.) The projected area of Earth, then, is
Thus, the power input from the Sun may be estimated as follows:
in excellent agreement with the 178,000 TW that Häfele [4] obtained before correcting for the Earth’s albedo, a, the fraction of power that is immediately reflected and, for all practical purposes, has no effect upon our CV. We computed the value 0.3 from Fig. 2-9 in Chapter 2, which was taken from Häfele [4]. We could have done a fancy calculation using integral calculus to account for the actual spherical nature of the wave fronts of the Sun’s radiation, but it wouldn't have affected our answer by more than a few percent.
Let Pi+ (= Psun) be the total radiation from the Sun that strikes the Earth’s CV per unit time. It is composed of two parts. The first part is
the portion that is reflected from the Earth’s CV or, perhaps, enters and leaves without having any effect upon the control volume according to a fundamental assumption of this study. It cancels out of our balance equations. The remainder of the solar power must be analyzed: