Overall Availability Analysis of Earth, Part 2
Table of Contents to Part 2
Computing the Lost Work or Maximum Reversible Work for Earth’s Control Volume (continued from Part 1)
Miscellaneous Fluxes and Other Things Calculated and Not Calculated
Average Grey-Body Emissivity of Earth
Difficulties and Uncertainties Due to Photons Not in Equilibrium and Irreversibilities
Computing the Lost Work or Maximum Reversible Work for Earth’s Control Volume (continued from Part 1)
[Note by Dave Bowman (8-4-97).
Due to the
albedo, the higher frequency radiation does not enter our computation,
therefore we may treat the Earth as more or less a black body with
respect to
the preponderant far-infrared radiation leaving the Earth in all
directions as
‘junk heat’ – except that most authors
would not treat this radiation as heat
in Second Law analysis because of the large irreversibilities due to
finite
temperature differences. Nevertheless, we use the heat-out
term in the First
and Second Laws Combined to pump power out of the CV from 
to 
later
on in this development.]
The
second part of 
is 
. Since
the Sun’s emissivity 
is taken
to be 1.0, the
portion of 
considered
in this study is (1
- a)
, the nature of which is well
enough understood because the albedo got rid of the more mysterious
higher frequencies.
Since
the far-infrared radiation emitted from the Earth as junk heat
behaves essentially as blackbody radiation, essentially because the
troublesome
radiation was rejected by the albedo, the emissivity 
= 1.0
also. And, despite
global warming, if it occurs, nature keeps the Earth sufficiently well
in
energy balance that we may claim that 
.
If
we subtract 
from
both sides to account for
the albedo, set 
let 
replace
by
,
use 
=
,
and note
that 
=
since
the Sun ‘sees’
the Earth (plus its atmosphere) as a flat disk of area 
, whereas
the Earth emits far-infrared radiation from its entire spherical
area 4 
.
The two areas differ by a factor of four; so, after we have canceled ,
we get 
.
,
which implies
,
Then,
.
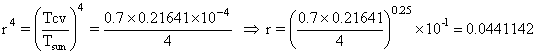Thus, =
0.0441142 
=
0.0441142 
5760
K = 254 K .
Tcv = 254 K .
This temperature may seem too low; however, we must not forget that the surface of the control volume is 100 miles above the surface of the Earth. The U-2 pilots tell me that it’s cold up there.
.
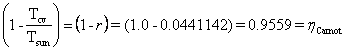Let’s
see how well 
matches the output 
.
which matches the input admirably. Thus,
This concludes our discussion of the First Law as it applies to photons. We should begin our analysis of the Second Law by writing an entropy balance over the entire Universe:
,
where
and
are
the rates at which entropy leaves and enters the control
volume. We have
agreed already that the CV shall be in steady state with respect to
entropy, so
.
Moreover, the Second Law tells us that 
must be
positive. Therefore,
the rate at which entropy leaves the CV may not be less than the rate
at which
entropy enters the CV, otherwise the rate at which the entropy of the
Universe
changes would be negative, which we know cannot happen. For
convenience, let’s
denote the minimum value of the rate at which entropy leaves our
control volume
as 
,
which, of course, is just
equal to 
.
We may
now introduce the appropriate First Law variables into our
Second Law discussion. According to Yourgrau et al. [5], the
entropy of a
photon gas can be written 
,
where 
is the
rate
at which internal energy enters the CV. Therefore,
,
since 
.
Then,
= 
= 
= 
.
Thus,
.
Eq. (I-10)
Equation
I-10 can be rewritten in terms of internal energies or
enthalpies, since H =
:
But, since Hi = He,
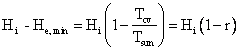
and
.
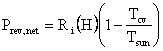Finally,
setting 
for
this calculation, we get
the thermodynamic lost power in two steps.
Normally, in engineering problems, To is the temperature of the coldest thermal reservoir (heat sink capable of absorbing unlimited thermal energy without changing temperature and, strictly speaking, differing in temperature from the CV only infinitesimally). Clearly, the heat transfer in the normal statement of the Second Law is reversible, but one can take some liberties in most practical applications. Engineers set To equal to the temperature of the air or the nearest body of water, whichever they are polluting in the case under consideration. The meaning of To is the temperature at which a heat engine rejects thermal energy.
The
first step was the simplified First Law calculation of 
involving
the difference in two enthalpies, the enthalpy of the photons entering
our CV
and the least enthalpy the photons might carry out of the CV without
violating
the Second Law. The second step was the work that would have
to be done by a
Carnot heat pump to raise the power entering the control volume from
254 K to
the environmental temperature 288 K; so that the world would be
restored to
what it would have been without irreversible activity. The
first step is like
replacing a bottle of champagne you have broken; the second step is
like
cleaning up the mess you made when you broke the bottle and got
champagne all
over the place. Whenever we try to compute the thermodynamic
lost power from
First Law variables, we must have some such step as pumping heat
– unless
everything is done precisely at To.
(If we make a mess at a
temperature appreciably higher than ambient, we can recover some of the
work.)
We shall now solve this problem in three slightly different ways using the Second Law exclusively.
Second
Law: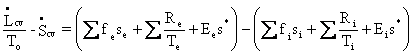 
,
Eq. (I-11)
where
s* is the constant ratio of mean entropy to mean number of photons for
a
macroscopic ensemble. Notice that, in this rendering of the
balance equation,
the rates of change of CV properties are isolated on the left-hand
side,
whereas the convection, conduction, and radiation terms (and only those
terms)
appear on the right-hand side, which is written in the form
‘out minus in’.
This equation is intended to be used in the steady-state case; i.e. 
=
0, and with no convection or conduction terms. Thus,
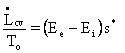
The
denominator in the lost work term in our entropy balance is ,
usually the temperature of the coldest heat sink we can find to which
our heat
engines may send useless exhaust heat as required by the Second Law,
represented as an entropy balance in Eq. I-11, above, where the rate of
change
of the entropy of the Earth is
,
the instantaneous rate of change of the product of the mass of the Earth (plus the mass of its atmosphere but excluding the mass of the core of the Earth) times the average entropy per kilogram of the Earth, indicated by angle brackets, as usual. Comparison of Ees* (large) to Eis* (small) explains how the Sun lowers the Earth's entropy. This is what allows life to exist on Earth.
Life is a process during which (roughly speaking) disorder is converted to order; i.e., high entropy is converted to low entropy. When the entropy is lowered within a living thing, it must be raised elsewhere in the environment. This could not occur over a prolonged period of time unless the overall entropy of the Earth were lowered somehow. The average frequency of the photons entering the Earth’s CV from the Sun is relatively high; therefore, since the energy of each photon is hn and the total energy of the photons entering is approximately equal to the energy of the low-frequency photons leaving, each photon has more energy and, consequently, the photons entering must be fewer in number.
(The
quantity 
,
cs = e or i, the number of
photons per second, equals the total energy per second divided by the
average
energy per photon. The symbol n
represents the frequency of the
electromagnetic wave associated with a photon and h is
Plank's constant, a “fundamental constant of the
universe” – according to many
physicists.) Fewer photons means fewer degrees
of freedom and a much diminished opportunity for chaotic behavior
(chaotic in
the old-fashioned sense of Boltzmann not in the
“modern” sense of Feigenbaum,
Lorenz, Kolmogorov, Moser, et al. [9]), which, in turn, means lower
entropy.
On the other hand, the low-frequency photons leaving the Earth are much
greater
in number and, therefore, have many more degrees of freedom, which
means
greater entropy. With less entropy entering and more entropy
leaving, the net
effect of the Sun is to lower the entropy of the Earth.
The irreversibility rate
is the thermodynamic
lost work rate
divided by .
Also, it is the mechanical
lost work rate divided by the
temperature of the CV – assumed isothermal, which is good
enough for our
purposes. Let us write the Second Law for the
Earth’s control volume as
follows:
.
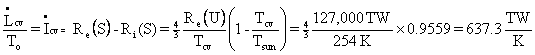Therefore,
.
Just as
a check, I shall solve the problem without using the relation 
.
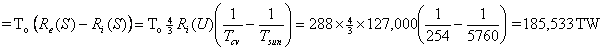
A final approach involves computing the number of photons leaving and entering per unit time.
Wien’s Displacement Law,
where μ is a micron and 1 micron = 10-6, is an easy way to get the wavelength corresponding to the maximum emission of radiative flux at a given temperature. It accounts for the color shift that we observe when a metal object, for example, is heated. Bowman was aware of the law that gives the average wavelength, λavg , at any temperature, as 1.838 ∙λmax. Thus, we can write λavg T = 5326.2 micron K. By using this modified Wien's Law for the black body radiation from the Sun at (effectively) 5760 K and for the infrared junk heat leaving the Earth’s CV at 254 K (resp.), we obtained 0.9247 microns and 20.97 microns (resp.) for the 70% of the Sun’s radiation not affected by the albedo and the Earth’s far-infrared radiation (resp.), for the average wavelength.
Finally, we can write the First and Second Laws Combined with its radiation terms represented by photons as follows:
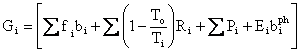
and
Ge
= 
where G stands for Gibbs. This leads to the incredibly terse statement:
.
Eq. (I-12)
The
First and Second Laws Combined was obtained by multiplying the Second
Law by and
subtracting
the product from the First Law.
Following De Nevers and Seader [10], we can make an interesting point with only a little more effort. Let
,
and
Fe
= 
,
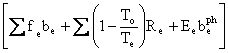so that we can write
,
Eq.
(I-13)
which gives 
, the reversible
power required
to obtain the same result from this CV that is obtained by any process
with (i)
the same inputs and outputs, (ii) the same change of state inside the
control
volume, and (iii) the same heat terms transferring heat at the same
temperatures to the same thermal reservoirs – with the
exception of heat
reservoirs at the temperature of the environment .
This may be
the maximum power or minimum power depending upon
circumstances. In either
case, it can be approached but never attained. It is the sum
of the
thermodynamic lost work and the net external work done by or done upon
the CV,
for any process – reversible or irreversible. If we
know (i) 
the
change of state of the CV, (ii) the heat transfer rates to each thermal
reservoir (other than the environment) and their temperatures, and
(iii) the
net power produced or consumed by the CV, we can compute (a) the
thermodynamic
lost power, and (b) the reversible power necessary to achieve (i),
(ii), and
(iii), that is, the reversible power – or, for a batch
(non-continuous)
process, the reversible work, which represents the unattainable ideal
for that
process.
Suppose
we compare our (real) process 
with a reversible
process 
,
with (i) the same streams entering and leaving, (ii) the same internal
changes,
and (iii) the same heat transfer to the same thermal reservoirs other
than the
reservoirs at .
Then, we see from Eq. I-12 that 
where 
; and,
therefore, 
. 
.
Thus,
the lost work for Process is just the
additional heat that
must be dumped to the environment at over
and above
that which must be dumped for Process .
Let us
consider the first term on the left-hand side of Eq. I-13: 
,
where 
.
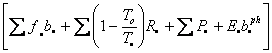It is the rate of accumulation of availability within the Earth and her
oceans
and her atmosphere and her biosphere, all of which are capable of
storing
availability. A particularly large storehouse of availability
is the
concentrated biomass represented by our coal, gas, and petroleum
deposits.
This took millions, if not billions, of years to accumulate; but,
during the
last two hundred years (particularly the last fifty years), we have
been
exhausting it at an alarming rate; therefore, it is virtually a
certainty that is
negative.
The åfibi term would represent only the negligible amount of debris that Earth picks up as it travels through nearly empty space – a few meteorites and some space dust. Likewise the Sfebe term represents only the small amount of availability associated with matter lost to space, particularly availability associated with hydrogen high in the Earth's atmosphere. For all practical purposes this term can be neglected too.
We have a relatively small amount of work done on the Earth by nearby gravitating objects – primarily the moon. Most of this work comes from the moon giving up some of its potential energy with respect to the Earth by moving a few centimeters away from the Earth each year. (The reader will recall from high-school physics that the gravitational force exerted by the moon upon the Earth is inversely proportional to the square of the distance between the moon and the Earth.) The Earth, correspondingly, does very little work upon her surroundings. Therefore, we shall neglect the work terms.
With current technology, we can tap geothermal energy at only a few isolated places on Earth. We shouldn't count on this energy anyway since it is not renewable, moreover we have no idea what the effect might be of cooling the interior of the Earth even slightly. Probably, the interior of the Earth is a more important scientific frontier than is outer space. My personal disapproval of space research, based on the past and current destructiveness of man’s activities on Earth, is discussed in my essay “On Space Travel and Research” in Vol. II of my collected papers [8]. Since the heat from the Sun and the heat radiated by the Earth (at approximately 254 K) are accounted for by the radiation terms, we may drop the conduction terms as well as the convection terms shown in Eq. I-13.
Finally, the lost work term represents all of the irreversibilities occurring in all of the subsystems of which the CV is composed. This includes the falling rain, the burning of fuels and forests, the turbulence of the winds and waves, the industrial activity of man, in fact, nearly every act of man and Nature. Almost every action involves some irreversibility and the only reason I say “almost” is because I want to be safe. Perhaps the reader can think of a completely reversible process that actually occurs. I cannot. Equation I-11 can now be written as follows:
.
Eq. (I-14)
This version of Eq. I-7 is useful for illustrating how the Sun increases the Earth's Helmholtz availability.
If we impose our condition of steady state with respect to Helmholtz availability, Eq. I-13 becomes
.
Eq. (I-15)
We may
write 
as
since
we
showed earlier that 
, then
,
Eq.
(I-16)
This
equation is restricted to quasi-equilibrium situations, simple
compressible substances, uniform state, and uniform flow by most
authors. De
Nevers and Seader [10], however, point out that the way the First and
Second
Laws Combined is set up here it applies to both reversible and
irreversible
processes. Other restrictions may apply. Let 
be
constant value of
the entropy to number of photons ratio. 
is, of course, a
positive
number, in a steady-state, adiabatic CV with negligible mass crossing
the
control surface – and (for the combined law) negligible
(gravitational) work
terms. Our estimate of is given above.
Also, it is the rate at which negentropy enters the CV, which is where many analysts would stop. But, it is the availability budget that tells us how much reversible work can be done and that's what we would optimize to minimize operating costs – unfortunately with the trade-off of infinite capital costs. We are using the language of capitalism, but we are doing Economics As If People Mattered [E. F. Schumacher] and we are looking at the items of legitimate interest to people – not at failed abstractions. The things we really need to live and the real costs to the environment of providing them are best measured in emergy units [Howard Odum]. (Emergy is based upon availability as discussed in Chapter 2.)
The availability of the photons associated with the incoherent infrared radiation constantly radiated from Earth in all directions into space is useless to Earthlings regardless of what space nuts may imagine. Hopefully, if they try to harness that low-grade energy, they shall be restrained appropriately. If the reader wishes, he can read Wayburn’s essay “On Space Travel and Research” [8]. We find the space scientists singularly selfish, inconsiderate of the needs of the rest of us, and really quite stupid. So much for the fabled rocket scientist and his latter-day cowboy myths. The myth of space research appeals to the romantic in all of us and to the credulity of the soft-minded. Soft-minded not necessarily weak-minded.
Since
Helmholtz availability is 
, if the
Earth is in
steady-state with respect to energy and with respect to Helmholtz
availability
too, then She is in steady-state with respect to entropy.
After we compute the
rate of lost work (power), we can compute (approximately) the increase
in
entropy we can allow because of irreversibilities. And everything
is irreversible. For now it is
enough to recognize that the First and Second Laws Combined will reduce
to the
same equations we used to compute the lost power using the Second Law
provided 
,
but we already know that 
It
would be pointless to
repeat the exercise, although the reader may do it if he wishes
(presumably
with the book closed).
It is
interesting to note that the lost power can be computed as the
work entering the Earth from a Carnot engine operating between the Sun
and minus
the heat leaving the Earth in the First and Second Laws
Combined. Begin with
,
where
,
=
,
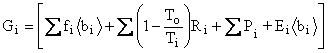and discard all the terms except the following:
.
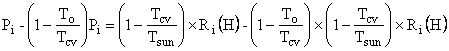Now, we can simplify the equation, but that might obscure what is going on. Let us plug numbers into it as it is.
.
Of course, what has happened is that we could have discharged heat at 254 K, but we were required to use the 288 K heat sink, which increased the lost power by about 13%.
Miscellaneous Fluxes and Other Things Calculated and Not Calculated
Fluxes
The
average solar flux absorbed by the Earth’s surface
is 
=
236 W / m2 ,
which is the same as the average far-infrared flux emitted from the
Earth’s
surface or upper atmosphere , 
= 236 W
/ m2.
Average Grey-Body Emissivity of Earth
Since
,
= 
I have no idea how useful or accurate such a grey body number might be. We include it for style only.
Solar Constant
The solar
constant, 
was
computed by Bowman as
follows: 
.
Difficulties and Uncertainties Due to Photons Not in Equilibrium and Irreversibilities
In none of Wayburn’s eight (engineering) thermodynamics texts could be found a decent treatment of radiative heat transfer. Normally it is not mentioned. A ninth book, from the library, Exergy Analysis of Thermal, Chemical, and Metallurgical Processes by Szargut et al. [11] devotes a few pages to radiative heat transfer, but appears to be a hopeless muddle. Most of the equations have the name for the right-hand side on the left-hand side; i.e., they are really no better than definitions and tautologies. Moreover, we am gradually getting the idea that every radiative process in the book must have a source or sink out of or into which heat is transferred by conduction. With all due respect and a touch of hyperbole, may we suggest to the authors of [11] that B is not the only letter in the Latin alphabet and that, when every variable is named B (for availability) and different variables are distinguished by 6-point subscripts, the authors strain the patience of older readers considerably. (Almost) nothing makes one feel like an old man so much as reading with a magnifying glass.
Wayburn just reviewed some articles on thermodynamic lost work and exergy, which is sometimes called availability, although it’s not exactly our availability, and sometimes called essergy. It seems that a minor war has been raging between the supporters of rival techniques. Apparently, though, each methodology has its uses. We are employing the lost work methodology in this appendix; however, in Chapter 2, Wayburn employed exergy quite profitably. The reader should be aware that, when we use the expression availability balance, we mean the use of Eq. I-7, which contains the term for the change in the value of the Helmholtz availability function within the CV. We are not referring to the availability that is defined to be the same as exergy. We apologize in advance for any confusion that arises due to the existence (in the literature) of two distinct concepts both referred to as availability. Most of this appendix had been written when Wayburn found out that exergy is sometimes called availability. We certainly wish no one would call it that. We shall call our availability the Gibbs availability function or the Helmholtz availability function except when those locutions give the sentence or the paragraph awkward metrical characteristics and no ambiguity can possibly arise.
Of Things Not Treated
In this brief introduction to thermodynamics, we avoided power cycles other than the imaginary Carnot cycle. Also, in a course in a chemical engineering department, a large chunk of time will be devoted to vapor-liquid equilibrium. This is the most difficult scientific information to obtain when designing sensitive separation processes. (One of the authors has seen with his own eyes a book of such data produced from photocopies and not exceeding 300 pages by much if any that was for sale at the time for $2,500 and sales were satisfactory. Normally, liquid-liquid equilibrium is treated too but not in quite so much depth. Many thermodynamics textbooks analyze mechanical and chemical equipment from pumps to reactors. This is way too nuts-and-boltsy for us. Finally, thermodynamics is the key to chemical reaction equilibria and, normally, a chapter is devoted to chemical reactions. In mechanical engineering departments, flow through turbines and nozzles, including supersonic flow and shock waves, is studied. Theoretical chemists and physicists seem to pay more attention to the fundamental mathematical relations and special relations among the distinguished partial derivatives derived from them. I believe I made in clear that the Second Law can be studied from the viewpoint of impossible processes, namely, the Clausius Statement of the Second Law and the Kelvin-Plank Statement. We don’t bother with these at all; balance equations are so much more useful.