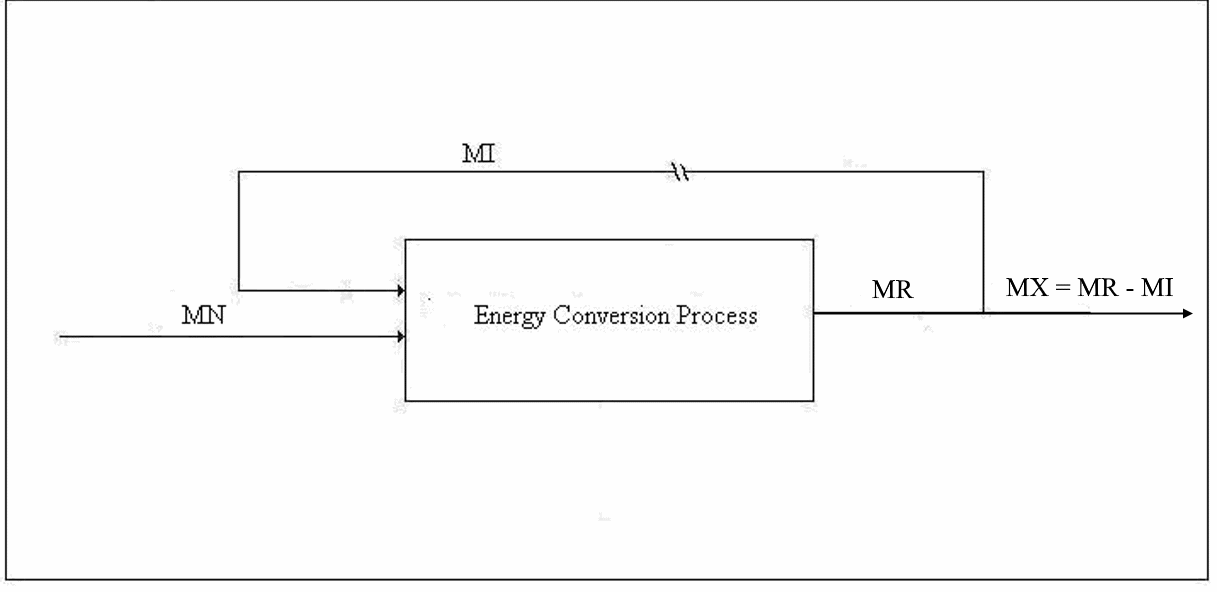
Figure 1. Emergy Balance for Type 1 Conversion
Thomas Wayburn, PhD
I will define availability, emergy and transformity as well as emergy efficiency and conversion or extraction effectiveness ratio. I assume that nearly everyone knows what ERoEI is; but, if you ask me, no one understands it. In the second and largest part of the paper, I will use balance equations to analyze a few simple process arrangements. Emergy efficiency relates the input to the outputs of these arrangements; ERoEI (Energy Reurned over Energy Invested) relates recovered product to the emergy of the process service inputs, both direct and indirect, rather than the direct input to solar panels or vanes of a wind turbine. The conversion ratio is a measure of the effectiveness of the principal mode of energy collection
Definition (Availability). Availability (or available energy) is energy [enthalpy, H, or internal energy, U] corrected for entropy, S. Rigorous definitions of the Gibbs availability function [H – ToS], the Helmholtz availability function [U - ToS], and entropy are given in Appendix I, Fundamentals of Thermodynamics, where the symbols and technical terms employed in this paragraph are explained. [To is the temperature of the environment, usually taken to be the temperature of the coldest body of water or the atmosphere into which the waste heat of a heat engine can be discharged. For Earth, 300 K will do. The effect of entropy on the availability function of sunlight is to reduce it by the ratio of the temperature of Earth to the temperature of the Sun – a factor of about 1/20, which gives an enthalpy of about 19/20 of the availability. Since the enthalpy of a photon is 4/3 times the energy, the Gibbs availability of sunlight is about 76/60 times the energy.]
Odum’s original definition of emergy. Odum defined emergy, measured in emjoules, to be the Gibbs availability of the sunlight, measured in joules, required to produce, by an optimal process, (1) fuels; (2) other energy sources such as wind or fresh water in mountain lakes; (3) natural resources such as grass and trees, (4) manufactured objects, (5) human resources; (6) information; and (7) any other objects of economic interest that can be associated with an identifiable quantity of sunlight. This is a sunlight-based emergy. It leads to large numbers for the emergies of primary fuels that are known only approximately; therefore, we shall modify the definition slightly to give common industrial energy products emergies that are known precisely and that are close to 1.0 in magnitude.
Definition (Standard Electricity). In this paper, single-phase, 60 Hz, 110-volt alternating current delivered to the user’s meter is taken to be standard electricity.
Definition (Emergy Unit). My arbitrary – but well-defined – choice for one unit of emergy (1 MU) is 1.0 kilowatt-hours of standard electricity. Although electrical current carries a small amount of entropy manifest in difference currents, for all practical purposes, that is, for engineering purposes, electricity is pure work. The availability of electricity is equal to its energy or enthalpy; and, with this choice of emergy unit, the emergy of electrical current is numerically equal to its energy in kilowatt-hours. The transformity of sunlight, wind, biomass, and other energy products will be less than – but close to – 1.0.
Definition (Transformity). The transformity of a primary fuel is the number of kilowatt-hours of standard electricity one can obtain from 1 kWhr of the primary fuel by an efficient process, the tradition of reporting the availability of fuels in BTUs per pound or kilocalories per gram mole notwithstanding. Any unit of energy can be converted to kilowatt-hours. This is an electricity-based transformity, the units of which are emergy units per kilowatt-hour.
Definition (Emergy). The embodied energy or emergy of a primary fuel is the Gibbs availability of the fuel in kilowatt-hours multiplied by the electricity-based transformity. The emergy of anything else is the sum of all the emergy that went into producing it by an efficient process minus the emergies of any by-products formed. The emergy of an activity is the average rate of expenditure of emergy times the time. These definitions are easily extended to include the dependence of emergy on location and time. The concept of nemergy or negative emergy can be introduced to aid in the discussion of environmental damage.
Definition (Emergy efficiency). Emergy efficiency of a manufacturing process is emergy out divided by emergy in. This efficiency is 1.0 for an optimal process because the emergy of the output is defined to be the emergy of the inputs. For a less than optimal process, the emergy efficiency is the emergy of the inputs to an optimal process over the emergy of the inputs to the process under investigation. Emergy efficiency lies between zero and one. A useful definition of emergy efficiency for the production or extraction of a fuel might be the emergy of the fuel plus the emergy of any byproducts divided by the emergy of all the inputs including the emergy supplied by nature. The energy supplied by nature is not considered part of the energy-invested term, otherwise an ERoEI greater than 1.0 could not be obtained; therefore, to characterize the process completely, an additional parameter that incorporates the direct input is needed. The efficiency incorporates the direct input to the process under investigation whether paid for or not.
Definition (Extraction or Conversion Effectiveness Ratio, m) This is the ratio of Gibbs availability returned per unit of Gibbs availability in the direct input to the technology whether the input is supplied by Nature such as wind power or is a primary fuel undergoing conversion. One realizes that the energy invested is not solar energy going to photovoltaic cells but everything else that is required to harvest Gibbs availability from sunlight in real time. We could call this ratio Energy Returned over Energy Converted, i. e., ERoEC.
Sholto Maud suggested working out energy, availability, and emergy balance equations for simple extraction and conversion processes. Writing balance equations for extraction and Type 1 conversion helped me understand what must be included in the definition of emergy and what may not be included without encountering inconsistencies. Inasmuch as some streams encountrered in net energy analysis are left with chemically active portions that normally are inconvenient to recover and normally are discharged with the waste, we do not expect to see balance equations for exergy. Also, see https://www.dematerialism.net/Mark-II-Balance.html.
Extraction. An example of extraction is the processing of petroleum from the well to the refinery. Extraction is discussed in https://www.dematerialism.net/Mark-II-EROI.html.
Type 1 Conversion. The first type of conversion is the production of primary energy from energy supplied by Nature for which we do not compensate Nature. The input to such a process includes other types of energy, material goods, transportation, labor, taxes, etc. The output includes the principal product, one or more by-products, waste heat, and pollution. Normally, pollution is not considered; however, the concept of nemergy (negative emergy) should be employed to account for pollution of every type even, for example, the extent to which animals are deprived of habitat by the mere existence of the energy production facility. Examples of Type 1 conversion are the production of electricity by wind power and solar power. The emergy balance equation for a Type 1 process will be discussed next:

Figure
1. Emergy Balance for Type 1 Conversion
Let us define some symbols to be used in connection with Figure 1: x
 xx
xx
Each of the input emergies is to be transformed into a product-equivalent emergy. Then, the “energy invested”, which should be called “availability invested”, EI, is imagined to have been produced by the same process that produced the product. In this way, it will be apparent immediately if the process consumes more available energy than it produces. All indirect energy expenses should be included in the EI term, in which case, simply because it is dimensionless, ERoEI* is a better measure of the effectiveness of the process than EX, the net availability produced. Looking at net product and ignoring ERoEI* might result in a large installation being favored over a much better small technology. [An example of an indirect cost is the pro-rata share of the commuting costs of the tax consultant (A) that should be charged to the worker (B) who maintains a wind power installation because the man (C) who serves B lunch had his taxes done by A.]
We are interested in two additional parameters, which can be computed, one from the other, using the emergy balance, namely, the transformity of the energy supplied by Nature and the overall efficiency of the technology under investigation. The governing equations for these are usually known – at least approximately. For example, the conversion efficiency of solar panels is a function of the angle of declination of the sun and the angle the sun's rays makes with the principal axis of the panel as well as the intensity of the insolation.
Hold the output emergy constant and allow the emergy supplied by Nature to increase to compensate for sub-optimal process.
Now, let us choose our control volume in such a way that the energy supplied by Nature is the only input and the net energy produced the sole output. Thus, for an efficient process, MN* = MX* (by definition) and λN* EN* = λR* EX*, since R, I, and X have the same specifications, including transformities. Finally, ER = m EN, where we want m as close to 1.0 as we can get it. This ultimately will determine the success or failure of the technology. However, even in the case where the value of m cannot be increased, a change in political economy as suggested in these papers will make a process successful that was a net consumer of energy in an American-style market economy. Suppose we choose a technology such that m = μ* is given. Then
and,
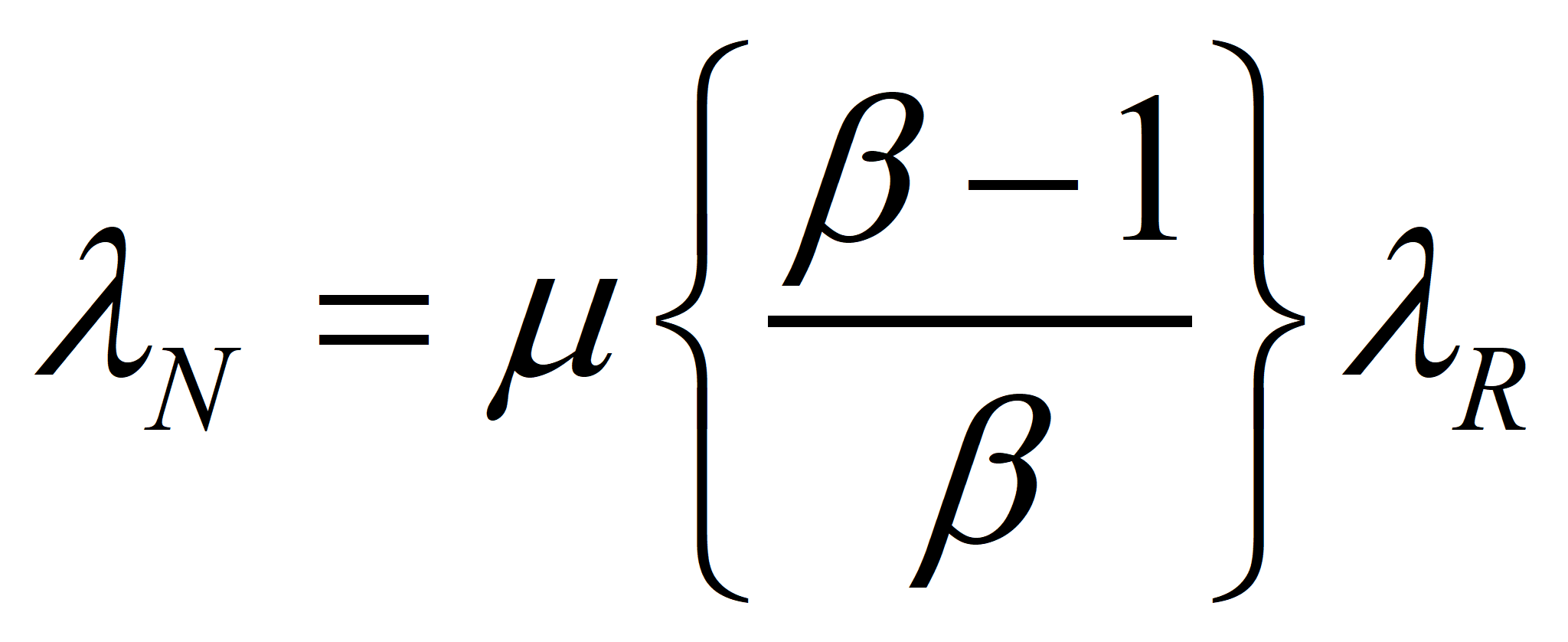
will give a good approximation of λN when λR is known.
We must now consider two possibilities:
Case 1. If λN, the value we compute, is greater than λN*, the accepted value of the transformity of the natural energy, then we should report that our process is part of a more efficient route to standard electricity, and λN should be considered for a new value of the transformity of the energy supplied by Nature.
Case 2. If λN is less than λN*, then our process is less efficient than the process that established the larger value and we must report an efficiency, η, for our process because we could have generated more emergy with the same quantity of natural energy if we had used the standard process. By definition, Nature supplies one unit of emergy per unit of emergy produced. If λN is lower, then our process used more available energy to achieve the same result as the optimal process. The following equation is approximately true if ER is close to ER*, which it will be in the case we care most about, namely, the case of ERoEI close to 1.0, with ER large compared to EX.
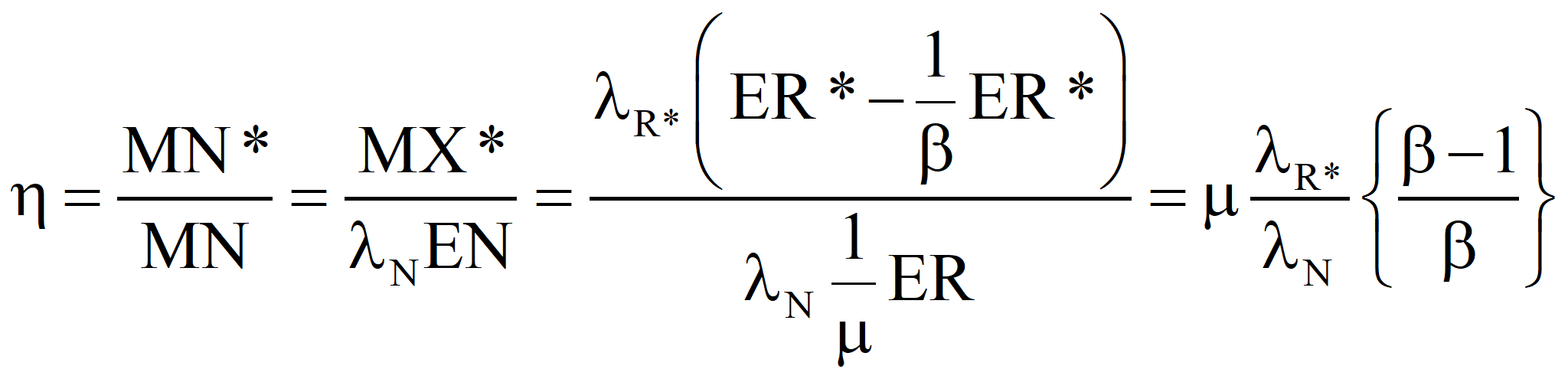
Hold the emergy supplied by Nature constant and allow less of the net product in the output of a sub-optimal technology.
In the second approach, the well-established value of the transformity of the energy supplied by Nature is accepted and the transformity of the product is computed from it. Call it λR'. If λR' is less than λR, the true value, we should revert to Case 1 and recalculate the transformity of the natural energy. If λR' is greater than λR, then the efficiency is as shown below:
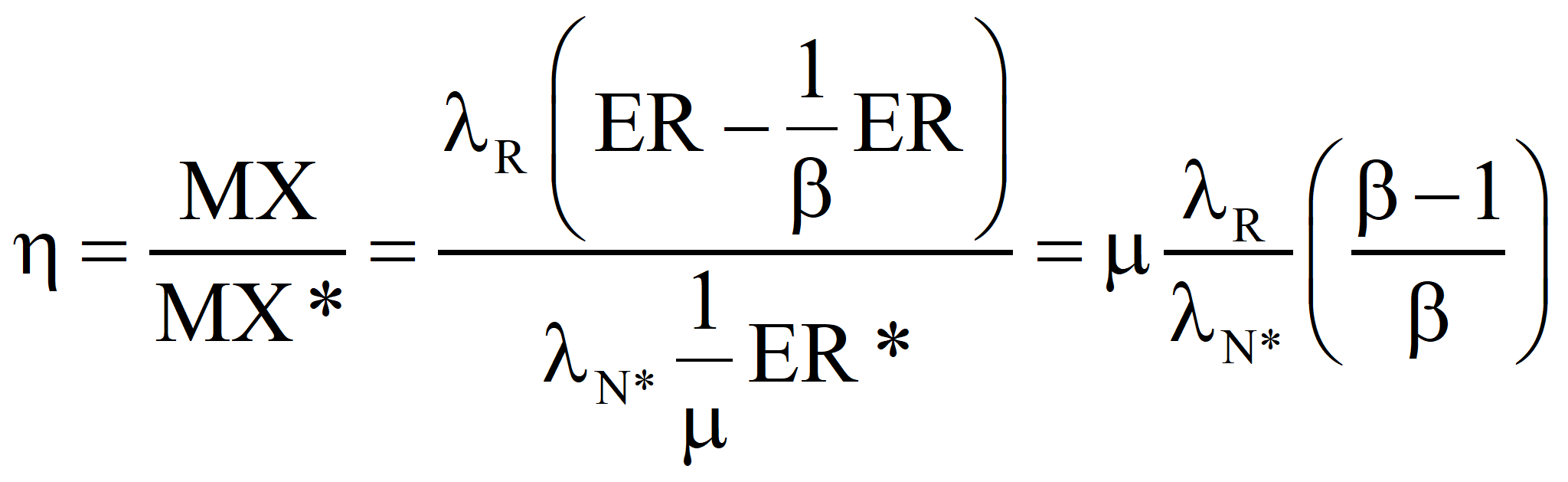
The infeasible case
Let us imagine the process in the configuration illustrated by Figure 2.
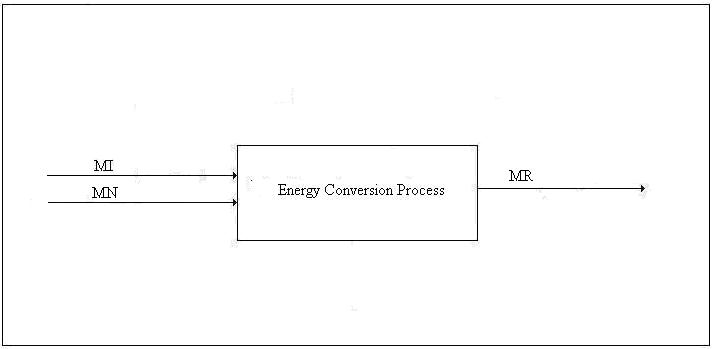
Figure 2. Alternative Diagram for Type 1 Conversion
If the algebraic sum of the emergy inputs to a process minus the emergy supplied by Nature exceeds the well-established emergy of the product, that is, if MI > MR, then the process is wasting energy resources. This is the case for some alternative energy projects that seek venture capital, government subsidies, donations, or unwary buyers. If they were not subsidized by fossil fuel, they would not work.
Produce secondary fuel by converting primary fuel.
Type 2 Conversion. The second type of conversion is the production of secondary energy from primary energy. The production of hydrogen from methane or from electrolysis of water is an example of Type 2 conversion. Figure 2 is the same as Figure 1 except that MP, the primary energy, is substituted for MN:
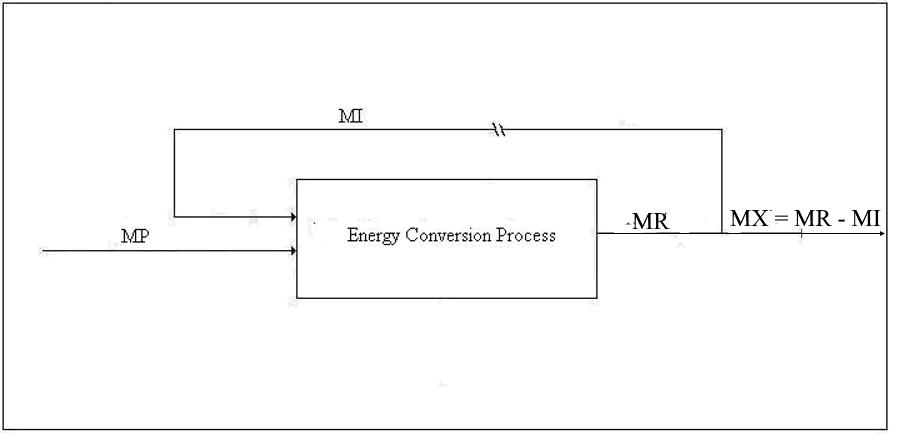
Figure 3. Emergy Balance for Type 2 Conversion
In the first approach, the transformity of the product is determined by the generation of standard electricity by a well-known efficient process and the transformity of the primary energy is computed from the emergy balance equation just as we did in the case of a Type 1 conversion, mutatis mutandis:
Case 1. If λP , the value we compute, is greater than λP*, the accepted value of the transformity of the primary energy, then we should report that our process is part of a more efficient route to standard electricity, and λP should be considered for a new value of the transformity of the primary energy.
Case 2. If λP is less than λP*, then our process is less efficient than the process that established the larger value and we must report an efficiency, η, for our process because we could have generated more emergy with the same quantity of primary energy if we had used the standard process.
In the second approach, the well-established value of the transformity of the primary energy is accepted and the transformity of the product is computed from it. Call it λR'. If λR' is less than λR, the true value, we should revert to Case 1 and recalculate the transformity of the natural energy. If λR' is greater than λR, then the efficiency is
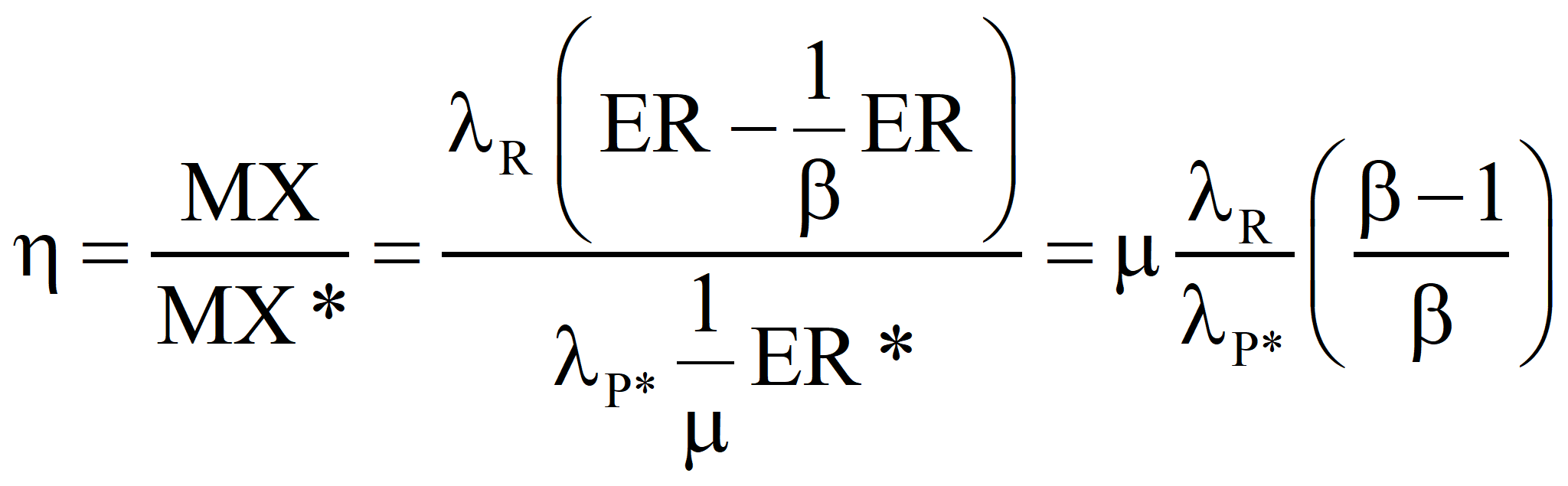
The case of constant product but more primary fuel required because of sub-optimality.
This is in agreement with the equation above. If a fuel the emergy of which is known is produced by the process under investigation and the sum of all of the emergy costs – both direct and indirect – that go into the process (computed with the true transformity λP*) minus the emergies of any useful by-products is greater than the algebraic sum of the emergy inputs for the process that determined the known emergy of the energy product, the process under investigation is sub-optimal and the efficiency, η, is
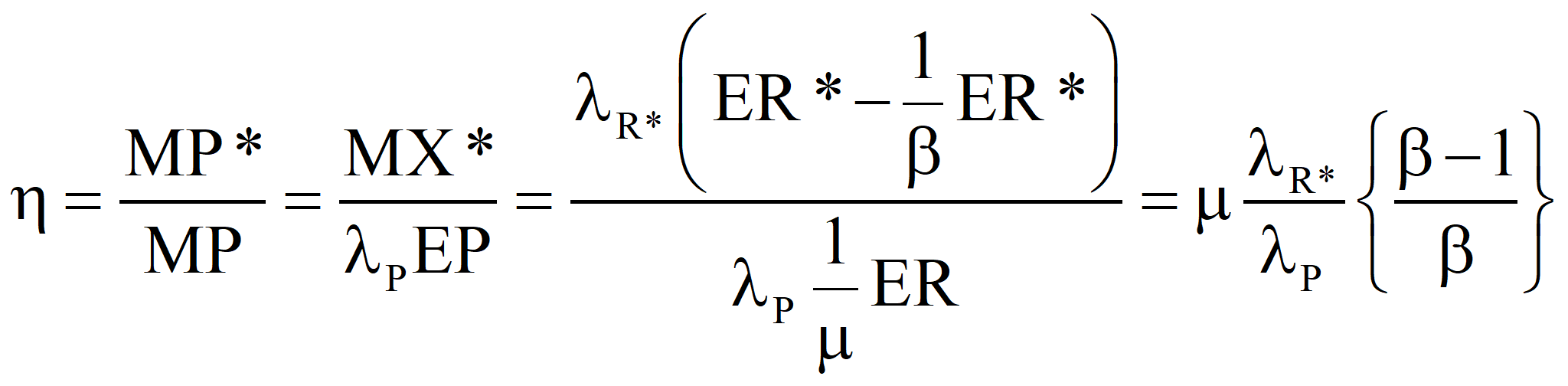
and, the transformity of the product we would compute from
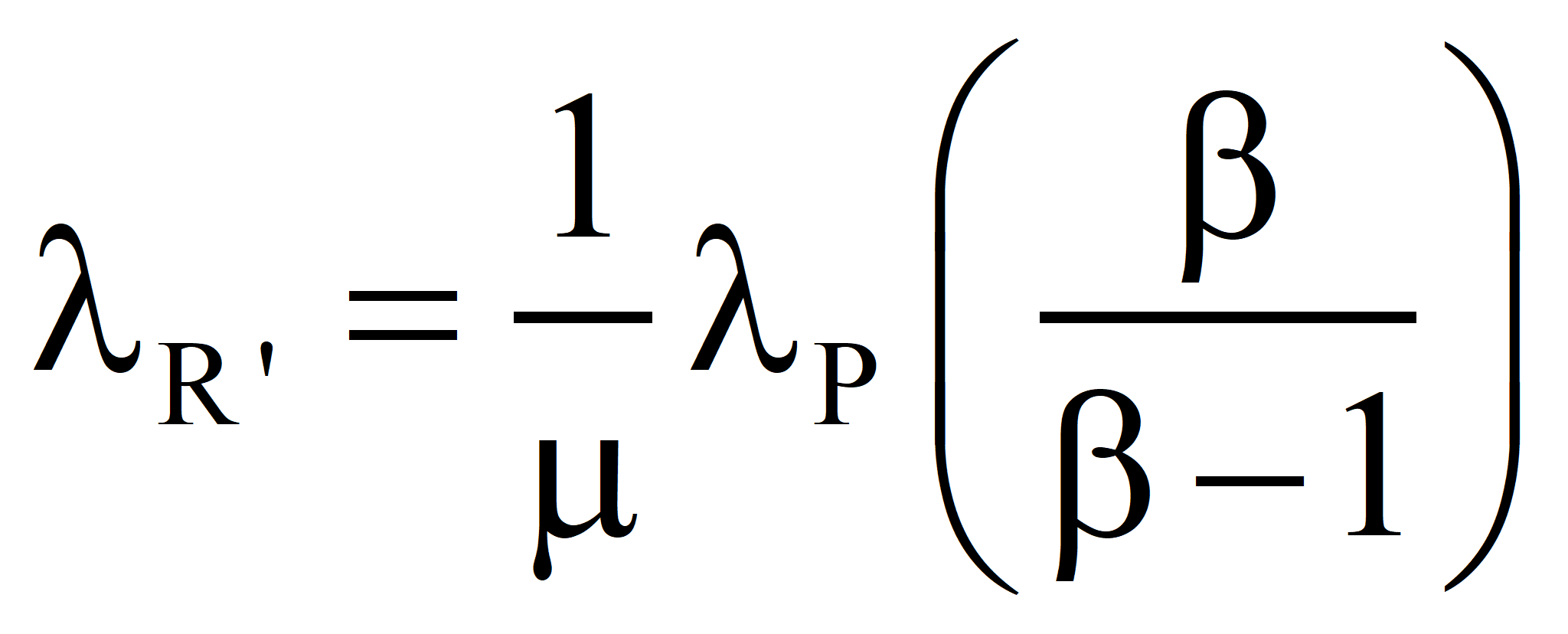
is higher than the true value λR. The only justification for the process is that we cannot do without the product and there is no other way to get it, which is not the case when electricity is used to produce hot water (discussed elsewhere) since hot water can be produced with less emergy by burning fuel under normal circumstances. Nevertheless, the process may be needed in extraordinary circumstances where the burning of fuel is prohibited, e. g., in a space capsule.
If the algebraic sum of the emergy inputs for the process under investigation is less than that of the older process, the transformity of the primary energy should be recalculated. It may not be expedient to discontinue production by the older process immediately because of compelling reasons not to shut down the older facilities – not the least of which is the time delay before new facilities can be built. The emergy efficiency of the older process is now less than 1.0.
Manufacture non-energy goods
Type 3 Conversion. The third type of conversion is the manufacture of non-energy goods. The manufacturing process has inputs of energy, material goods, transportation, labor, taxes, etc., and outputs that include a principal product, one or more by-products, and waste heat. This is best illustrated with a diagram such as Figure 4.
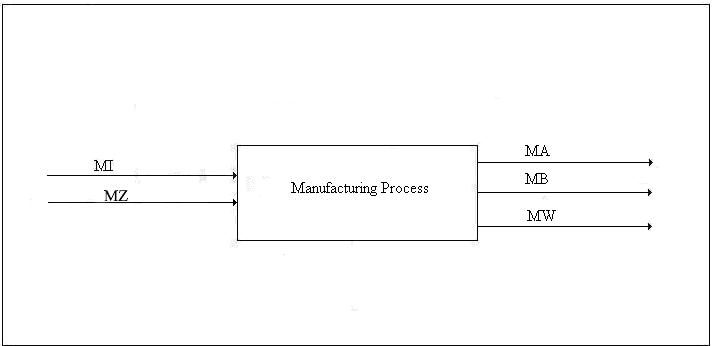
Figure 4. Emergy Balance for Manufacturing Process

The emergy, MW, of the waste heat stream is its availability times the number of kilowatts of standard electricity that can be generated efficiently by one kilowatt-hour of waste heat. The emergy of the sum total of all direct energy inputs to the process is determined in the usual way. The emergy of the sum total of all non-energy inputs must be available from past studies or must be determined during the analysis. It may include contributions from pollution etc. in which case negative emergy in the output is added to the input. Unlike the case of energy production, the transformities of the inputs cannot be influenced by the process. The emergy of the principal product and the by-product must equal the emergy of the inputs minus the emergy of the waste heat. In the case of a principal product as the sole output, the determination is trivial. However, when one or more by-products are present, the emergies of the by-products and the principal project must be apportioned in a canonical manner that should be determined by the analyst on a case-by-case basis.
If the emergy of a by-product is known in some other way, it may be appropriate to use the known value. In a case where the emergies must be distributed equitably, the relation between market price, either instantaneous or averaged over time, and energy or emergy may be useful. See “The Relation of Energy to Money”. Thus, the emergy is apportioned according to market value. This is a singular intrusion of money into the physical realm of emergy analysis and may not be advisable. In a non-market economy, some combination of energy, labor, capital expenditures, product mass or heat of fusion (even) might be of use. In any case, the sum of the emergies of the products must close the emergy balance. The consumer may find it expedient to compare the emergy of any given product with the emergy of a comparable product to minimize his impact upon the environment.
Note. The reader should realize that the terms Type 1, Type 2, and Type 3 Conversion have no currency outside of this paper
Houston,
Texas
Friday, October 27, 2006
ERoEI -1 has been replaced by
ERoEI, and the conversion ratio, m,
has been redefined: May 8, 2020