THERMODYNAMICS, AVAILABILITY, AND EMERGY

Thomas L. Wayburn, PhD in chemical engineering

Table of Contents

Abstract

Introduction

Balance Equations and Availability

Emergy

Emergy and Efficiency

Emergy Analysis of Economies

Emergy Supply and Demand

A Little Arithmetic

Conclusions

References

 

Abstract

After a brief introduction establishing the need for emergy analysis, we begin by combining the First and Second Laws to get a definition of availability.  This motivates Odum's theory of emergy and transformity, which we use to model the U.S. or world economy and to speculate on an improved humanistic economy.  We indicate how one might go about determining the emergy costs of energy using nuclear fission as an example.  We then look at energy flows on the earth to estimate how much sustainable energy (availability) we can hope for in the best possible case (short of cold fusion).  We speculate that renewable energy from biomass is likely to be the major provider of energy toward the end of the next century.  We, then, look at how energy is likely to be distributed in a one kilowatt per capita, high-tech, neo-tribal, decentralized society and introduce the matching problem.  Finally, we consider under what conditions sustainable energy is likely to be sufficient to permit sustainable happiness - at least absence of unbearable misery - for ten billion people.

Introduction

Industrial civilization has been based on fossil fuels.  Currently, society is challenged by two opposing trends: (1) fossil fuel is running out and (2) developing nations (and poor people in rich nations) want to live the "American dream".  Americans have been bingeing on fossil fuel for 150 years - particularly on oil since World War II.  We have behaved like the heir who squanders in a day a large fortune built up over dozens of generations.  Even conservative analysts such as Wolf Häfele [1] predict severe oil shortages beginning around 2030.  The most "optimistic" estimates of total reserves - both discovered and undiscovered - would have us running out in about 100 years at the present rate of consumption assuming (1) no population growth and (2) continued disproportionately low use of oil in the third world.  This scenario is in severe conflict with the aspirations of many people.  Americans use 25% of the world's energy budget while comprising only 5% of the world's population.  Moreover, the American dream is an environmental nightmare.

Some people (usually not technologists) believe that shortages of fossil fuels will be relieved by technological breakthroughs.  It has been noted that these people are like smokers who won't quit because by the time they get cancer a cure will be found!  It has taken nature millions of years to evolve the tree.  The likelihood of man developing technology superior to a tree is only slightly greater than the likelihood of developing an artificial human being.  Actually, the horrifying plentiful-energy scenario with its excessive motion, alienation, and stress, if not pollution and the wiping out of nearly every species of plant and animal, is unlikely.  Reasonable quantities of renewable energy will be needed to support human life.  But, money is an inappropriate measure to determine which sustainable energy technologies will be feasible.  Prices are distorted by fossil-fuel subsidies.  According to Odum and Odum [2] we purchase the 1700 kilowatt hours (kWhrs) in a barrel of oil with the money obtained by expending only one-sixth of 1700 kWhrs.  Money does not account for the work done by nature; moreover, it does not satisfy useful conservation laws.  We need an energy-based measure of value such as emergy - with an m.  The Odums show that nuclear fission and, for that matter, photovoltaic cells are net consumers of energy.

Emergy analysis, despite its drawbacks, will achieve at least three goals: (1) it will enable us to determine the efficiencies of sustainable energy technologies, which, in turn, will permit us to establish the emergies of their products; (2) it will teach us economic "facts of life" that reveal why almost all public policy is irrational; and (3) emergy analysis will enable us to determine good policy and provide arguments toward widespread acceptance of reasonable social goals.  This, then, is an attempt to establish methodologies to put public policy on a firm scientific basis.

Balance Equations and Availability

Equation 1 is the First Law of Thermodynamics for a uniform-state, uniform-flow system written as a simplified energy balance with kinetic energy and gravitational potential energy neglected.

                          

The left-hand side is the accumulation within the control volume (CV) with the mass at the end of the experiment, m₂ , times the internal energy, u₂ , minus the same product at the beginning of the experiment.  Energy and injection work associated with mass, m_i , entering the CV and mass, m_e , leaving are represented by the enthalpy, h.  Heat entering the CV is Q_cv = SQ_i and work leaving is W_cv .

The Second Law is written as an entropy balance by introducing the thermodynamic lost work, LW_cv , which is the entropy change ∆S_irr due to irreversibilities within the CV times the temperature of the environment, T_o .

                

If we multiply Eq. 2 by T_o and subtract the result from Eq. 1, we get the availability balance, Eq. 3,

       

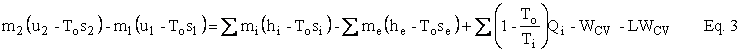
where a = u - T_os, the Helmholtz availability, and b = h - T_os, the Gibbs availability.  These quantities represent limits on the ability to do useful work.

                   

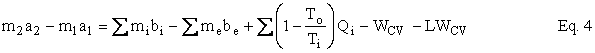
Equation 5 is Eq. 4 written as a rate equation with A = ma.

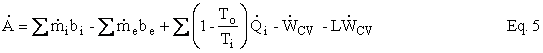
Using Eq. 5, we can show that, if the greenhouse effect produces unacceptable climate change, we will have to consume fossil fuels and dissociate CO₂ with close to 80% efficiency in order to break even.  It is unlikely that such efficiencies could be met, therefore we would have to discontinue the use of fossil fuels.

Emergy

In any case, we need to refer the availabilities of common fuels, especially renewable fuels, to an agreed upon standard, since a joule of Gibbs availability from diesel fuel cannot be obtained from a joule of Gibbs availability from sunlight.  In fact, it takes about 40,000 joules of sunlight to produce a joule of diesel fuel.  Howard Odum [3], the famous ecologist, uses emergy analysis to assign standardized values to things of interest to society.  His reference standard is one joule of sunlight.  Emergy measured in emjoules is the Gibbs availability of the sunlight, measured in joules, required to produce, by an optimal process, (1) fuels; (2) other energy sources such as wind or fresh water in mountain lakes; (3) natural resources such as grass, trees, and fossil fuels; (4) manufactured objects, (5) human resources; (6) information; and (7) any other objects of economic interest that can be associated with an identifiable quantity of sunlight.  In Table 1, typical transformities necessary to compute emergies based on sunlight are given.  Sunlight-based emergies have the disadvantage that they are large and known only very roughly.  Moreover, gross estimates are used to evaluate  the fuels we use most frequently.  We don't know how many joules of sunlight must be expended by the most efficient process to produce one joule of alcohol from biomass.  Undoubtedly, the optimal process has yet to be discovered.  These are deficiencies in emergy analysis.  In their earlier work [2], Howard and Elisabeth Odum measured emergy in fossil-fuel equivalents.  Emergies used to evaluate industrial economies might be computed more easily by taking the transformity of crude oil or even methane as unity.  If we are moving toward an electrical basis for energy analysis, it might be better to take one joule of 60 cycle AC current as the unit of emergy - or, perhaps even better, 3,600,000 joules ( = 1 kWhr).

 

Emergy and Efficiency

Emergy efficiency is emergy out divided by emergy in.  This efficiency is 1.0 for an optimal process because the emergy of the output is defined to be the emergy of the inputs.  Energy production efficiency is often taken to be energy out minus energy in divided by energy in with the energy supplied by nature ignored!  One can have negative energy efficiency, but  emergy efficiency lies between zero and one.  To compute the total emergy input of nuclear fission, we must consider all phases of the operation from discovery of uranium to the disposal of the decommissioned plant and the storage of radioactive materials for thousands of years.  If we hypothesize a world wherein all the primary energy is electricity from fission and the emergy input exceeds the output, our hypothesis is untenable; and, nuclear energy is infeasible.  (On December 27, 2005, we still don’t know if it’s feasible, since no nation has used nuclear energy without a generous infusion of fossil fuel.)  Even in the case of feasibility, if the emergy costs overwhelm the emergy costs of sustainable routes to electricity, nuclear fission should be rejected, unless our energy consumption has exceeded Maximum Renewables.

For the sake of simplicity, we divide the economy into four sectors, namely, energy, production, service, and business.  (Government is considered part of business.)  To the ith sector one assigns an emergy relation for each hour worked: e_i = e_w,i + a_ie_p,i , where e_i is the average total emergy expended per person-hour, e_w is the emergy expended at the job, and a_i is the fraction of the personal emergy budget, e_p , that must be charged to the job.  This methodology is promising because employment figures are readily available and the average emergy expenditure per employee can be estimated closely enough.

We then count the person-hours expended within the energy sector, E₁, the hours expended in the production sector, P₁, that must be charged to the energy sector, the hours in the service sector, S₁, that must be charged to the energy sector and the production sector, and the hours in the business sector, B₁, that must be charged to the energy, production, and service sectors.  But, P₁, S₁, and B₁ must be serviced by additional person-hours, E₂, from the energy sector, which hours, in turn, must be serviced by the production sector, P₂.  This second level of hours spent in the energy and production sectors entails additional work, S₂, in the service sector and all three require additional hours, B₂, spent in the business sector.  Secondary person-hours are followed by tertiary hours until no new hours can be identified.  This iterative accounting procedure must converge eventually because the total person-hours in the economy is finite over a finite length of time, which may not exceed the period of decay of the radioactive materials.  This difficult calculation can be carried out in principle; but, undoubtedly, excessive emergy costs will be encountered in many cases early in the process.  The exact mathematical procedure and the accompanying diagrams are omitted.  Please refer to Chapter 2 of On the Preservation of Species, which, incidentally, has better renderings of the figures copied below.  Also, Appendix I, Introduction to Thermodynamics, might be helpful to some readers.

Emergy Analysis of Economies

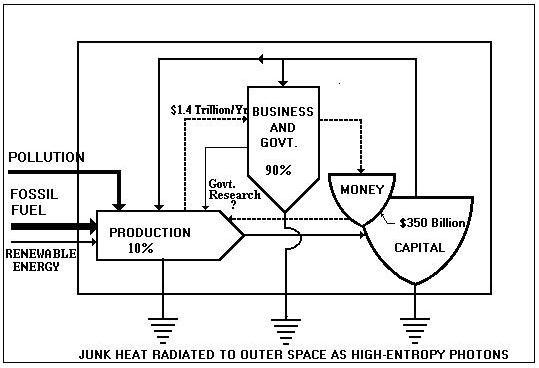
Figure 1. Odum's Emergy Diagram for Economy

Regardless of the basis chosen and in spite of the difficulties, we can use emergy to analyze the U.S. or, indeed, the world economy.  This is represented in Fig. 1 as a system diagram.  In Fig. 1 the emergy from fossil fuel is represented by a thick arrow entering production from the left-hand border.  The emergy of manufactured objects is stored in a capital pool and, in part, is recycled to production.  If the portion recycled is sufficiently great that the means of production can be enlarged so that more emergy can be drawn from the environment and more products produced, we say that we are capitalizing; i.e., we have capitalism in the strict sense.  Capitalization can occur globally when the supply of emergy from the environment is essentially infinite, but what we are experiencing now is a gradual shrinkage in the net amount of emergy available from the environment; i.e., we must go out to sea to find oil or transport oil over long distances.  Also, we must pay more emergy to restore the environment in case we spill oil or strip mine coal, for example.  In addition, we have a very expensive government (lumped together with business in the center of the diagram) that consumes a great deal of emergy that might have gone toward improving production.  The arrows going to junk heat represent depreciation, consumption, and excess emergy used by less-than-optimal processes.

In an emergy limited world, capitalism cannot exist.  Nevertheless, business people do their best to keep the money cycle (shown in Fig. 1) turning counter to the emergy cycle as fast as possible.  The faster the money cycle turns the more money they acquire even though they produce only negligible emergy.  Since the emergy cycle cannot be accelerated, we have what is known as inflation, i.e., less emergy per dollar.

In this type of economy, the people are regarded as belonging to production, business, government, etc. by virtue of their jobs.  The proportions are represented by the percentages on the drawing.  Clearly, an inordinate effort is consumed by business and government.  Eventually, people begin to lose jobs; the infrastructure begins to decay; and society reverts to barbarism.  This is a dog-eat-dog economy

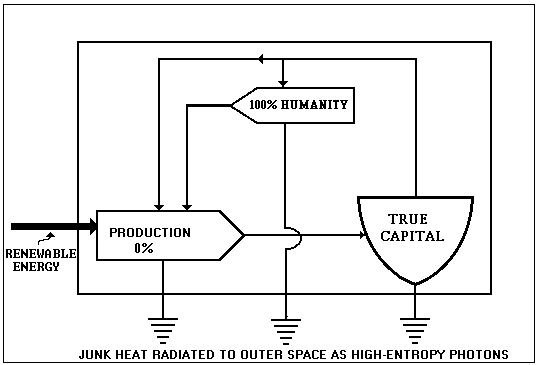
Figure 2. Emergy System Diagram for a Humanistic Economy

In the humanistic economy diagrammed in Fig. 2, competition for wealth and power has been abandoned.  People receive their fair (equal) share of the national (or world) dividend regardless of the activities they pursue, therefore they are no longer regarded as belonging to their jobs and the overhead of business and government is saved.  The only wealth is true wealth (emergy), which cannot be hoarded.  The economy is intentionally permitted to reach steady-state; production serves people who belong to themselves; and the only motivation is intrinsic motivation - as opposed to greed and fear.  Involvement replaces employment.

Emergy Supply and Demand

Figure 3 shows the flows of energy in the earth.  The only concession to emergy is the identification of the "high-quality" flows from wind, run-off (hydroelectric), heat convection (geothermal), and agriculture (biomass, including silviculture).  Is it realistic to expect to harvest even 10% of the energy captured by photosynthesis without extinguishing animal life?!

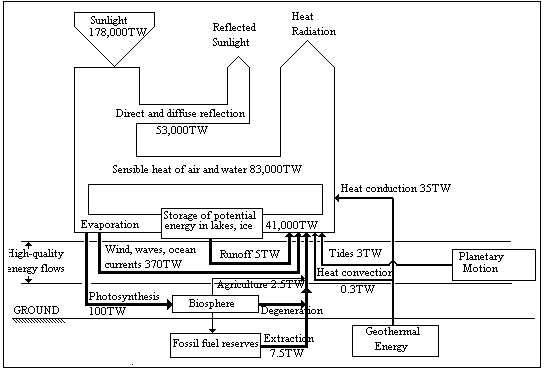
Figure 3. Energy Flows in the Environment [1]

We would now like to use the concept of emergy to estimate the standard of living in an economy driven by sustainable energy - a world where fossil fuel has been exhausted or may not be used because of global environmental effects or where prudence and common decency dictate that fossil fuel be preserved for future generations and better uses.  The best estimates (hard technological limits) for sustainable energy were evaluated in a massive effort by the International Institute of Applied Systems Analysis [1].  A few crucial results appear in Table 2 .

 

By 2030, the population of the world is expected to exceed ten billion souls [4].  We have approximately 10 billion kilowatts, which must be distributed equally among 10 billion people to avoid widespread famine and misery, i.e., 1 kilowatt/capita.  (Besides the obvious immorality of policies that tolerate widespread misery, Machiavellian pragmatism dictates that large numbers of miserable people will be a continuous danger to people who are well off - unless genocide is employed.)

Table 3 shows a conjectured expenditure of a 1 kilowatt (kW) energy budget without any attempt to solve the emergy matching problem, which, of course, will vary from region to region.  (We would not want to use biogas to generate electricity for electric stoves, since nearly everyone prefers to cook with gas.)  For the sake of argument, let us suppose that the matching problem, which will require a great deal of research, is solved.  If we need 0.05kW for cooking, we will have 0.05kW of biogas; if we need 0.15kW for bathing and comfort heating, we will have 0.15kW geothermal or passive solar.  We actually eat slightly more than 0.1kW biomass, although some energy remains after we have eaten it; but, for this analysis, it is assumed that somehow we can restrict our use of liquid fuels for agriculture to another 0.1kW.  (Currently, we consume between 0.25kW and 0.6kW overhead on food.  Ten gallons of gasoline per week amounts to 2.0kW of availability, which neglects the emergy costs of producing gasoline.  This is high-emergy consumption.)

 

A Little Arithmetic

It is easy to see that fewer than 10% of the projected population of the earth in 2030 can spend energy at the current American rate, under the condition that the remaining 90+% subsist on 0.3kW.  Moreover, for each person within the subsistence class who exceeds his allowance someone must die!  If the current populations of the U.S., Europe and Japan survive and all else perish, the surviving population must still spend less than 90% of the current American energy budget.

Suppose the existing oil reserves extend to the generous upper bound of 10,000 billion barrels.  (The highest estimate I could find was 5,600 billion on page 53 of Häfele's book [1].)  Suppose, further, that the population of the earth stabilizes at ten billion people for the next one hundred billion years - until the sun burns out.  Given a long life span of 100 years, 100 million people are born in each of 100 billion years giving a grand total of 10 × 10¹⁸ people who are entitled by every natural and moral law to share the 10 × 10¹² barrels of oil.  That gives one millionth of a barrel per person, i.e., essentially none.  (In this calculation we neglect new petroleum created constantly, but slowly, by nature.)  Suppose everyone alive in 2030 spent energy at the present American rate.  This would require an increase of five times (to account for the "improvement" in the lives of non-Americans) and an increase of double (to account for the increase in the population) giving a factor of 10 without counting increased energy use to prevent air and water pollution.  Even with the generous estimate of 10,000 billion barrels of oil left, we would run out in fewer than 20 years, i.e., before 2050.  Of course, the environment would be destroyed before then - unless perhaps half of the energy were devoted to reducing pollution, in which case we would run out in ten years.

Conclusions

1.       Fossil fuels should be used to eliminate the need for fossil fuels.

2.       Barring a highly improbable "technical" solution, energy budgets in the future will be much lower than they have been during the industrial era.  Probably, industrial civilization is ending.

3.       Due to moral, aesthetic, and pragmatic considerations, wealth (measured in emergy) will be distributed equally among all people in the world.  World federalism may be needed to redistribute natural resources appropriately.

4.       Political changes have to occur to prevent the rise of tyrants and totalitarian systems of government.

5.       To achieve these political changes, to minimize transportation costs, and to manage ecologies effectively, people will live in decentralized eco-communities.  The new societies might be referred to as neo-tribal, high-tech firewood societies - not because firewood will be burned (although it might be) but because renewable biomass is likely to be the energy basis of human activity, just as it was before this bizarre, alienating, dehumanizing, but blessedly short, period in human history known as the industrial revolution.  (This is the soft-energy viewpoint.  Other viewpoints exist.)

March 15, 1993

References

1.       Häfele, Wolf, Editor, Energy in a Finite World, Ballinger, Cambridge, MA, 1981.

2.       Odum, Howard T, and Elisabeth C. Odum, Energy Basis for Man and Nature, McGraw-Hill, New York, 1976.

3.       Odum, Howard T. and Jan E. Arding, Emergy Analysis of Shrimp Mariculture in Ecuador, Center for Wetlands, University of Florida, Gainesville, FL 32611, 1991.

4.       Population Studies No. 106, World Population Prospects 1988, United Nations, Dept. of Intl. Economic and Social Affairs, New York, 1989.