Balance Equations for Energy Extraction and Conversion
Table of Contents
Energy Balance
We shall refer to the figure below in the discussion of the energy balance.
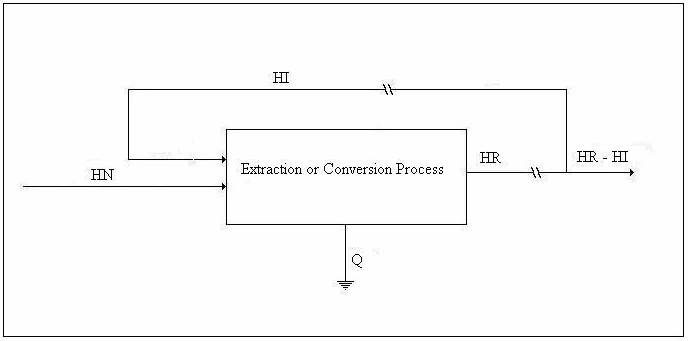
Figure 1. Drawing for Energy Balance
The well-known energy balance equation for an open system or, as I like to say, a control volume is as follows:
![]()
where U is internal energy, H = U + PV is enthalpy, W is work, and Q is heat. The subscripts i and o refer to in and out. Equation 1 is the First Law of Thermodynamics for a uniform-state, uniform-flow system written as a simplified energy balance with kinetic energy and gravitational potential energy neglected. The left-hand side is the accumulation within the control volume (CV) with the internal energy at the end of the experiment, U2, minus the internal energy at the beginning of the experiment, U1. Energy and injection work associated with mass entering the CV and mass leaving are represented by the enthalpy, H. Heat and work entering and leaving the CV are represented by Q and W.
In the case of simple steady-state extraction and conversion processes such as we are likely to encounter in the production of primary energy, Eq. 1 reduces to
![]()
or, in terms of the above drawing,
![]()
Let HR/HI = β and HN/HR = μ1. Then
![]()
or
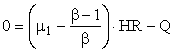
where we have used the fact that streams HR and HI have identical physical properties.
Entropy Balance
We shall refer to the figure below in the discussion of the entropy balance.
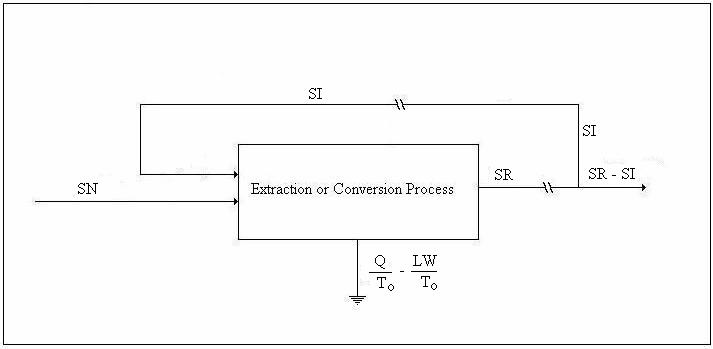
Figure 2. Drawing for Entropy Balance
The Second Law can be written as an entropy balance by introducing the thermodynamic lost work, LWcv , which is the entropy change ∆Sirr due to irreversibilities within the CV times the temperature of the environment, Te . Under reasonable assumptions, the equation for an open system or, as I like to say, a control volume is as follows:
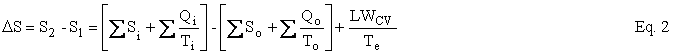
where U is internal energy, H = U + PV is enthalpy, W is work, Q is heat, T is temperature, and LWCV term is the irreversibility, which is added to achieve closure on the entropy balance and which allows the Second Law of Thermodynamics to be written for an open system. The subscripts i, o, and e refer to in, out, and environment. In our case, Te = To. In the case of simple steady-state extraction and conversion processes such as one is likely to encounter in the production of primary energy, Eq. 1 reduces to
![]()
or, in terms of the above drawing,
![]()
Let SN/SR = μ2; and, since SR/SI = β,
![]()
or
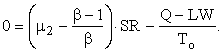
Availability Balance
We shall refer to the figure below in the discussion of the availability balance.
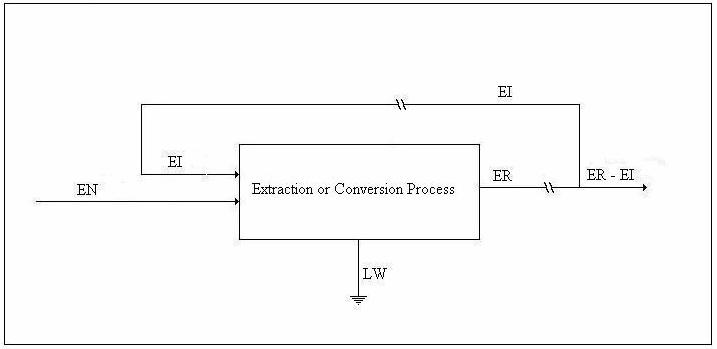
Figure 3. Drawing for Availability Balance
Helmholtz availability is U – TeS = A and Gibbs availability is H - TeS = E; therefore, the availability balance, which is obtained by multiplying the entropy balance equation by Te and subtracting it from the energy balance equation, is as follows:
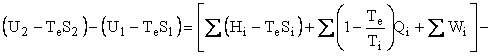
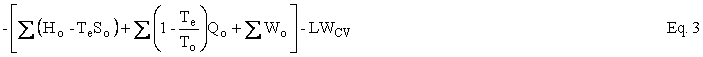
where U is internal energy, H = U + PV is enthalpy, W is work, Q is heat, and T is temperature. The subscripts i, o, and e refer to in, out, and environment. In our case, Te = To. In the case of simple steady-state extraction and conversion processes, such as one is likely to encounter in the production of primary energy, Eq. 3, with Te = To, reduces to
![]()
or, in terms of the above drawing,
![]()
Let EN/ER = μ; and, since ER/EI = β,
![]()
or
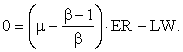
The ratio of EN to ER, μ, can be written in terms of μ1 and μ2 as follows:
![]()
This is the Combined First and Second Laws of Thermodynamics.
Emergy Balance
We shall refer to the figure below in the discussion of the emergy balance.
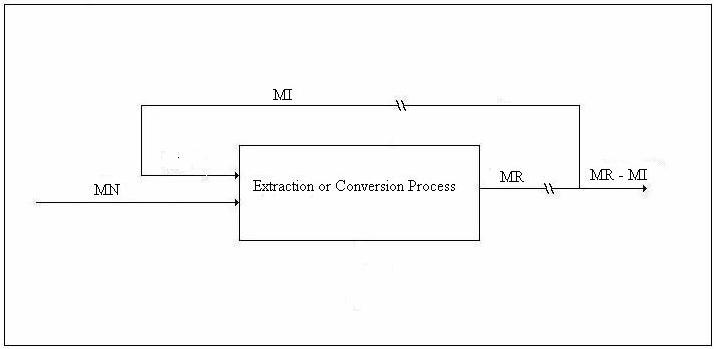
Figure 4. Drawing for Emergy Balance
Let MN be the emergy of the work supplied by Nature, MR the emergy of the immediate energy product, and MI the emergy of the energy investment stream. Let λN be the transformity of the energy supplied by Nature and λR the transformity of the immediate energy product (as opposed to MR – MI, the emergy delivered to the economy). The transformity, λi, is the number of kWhrs of single-phase, 60 Hz, 110-volt AC electricity one can obtain from 1 kWhr of energy source i by an efficient process. Thus, 1.0 kWhrs of single-phase, 60 Hz, 110-volt AC electricity is my (arbitrary, but well-defined) choice for the unit of emergy and λi is an electricity-based transformity. Then, since
![]()
![]()
or,
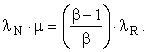
This relation can be used to find any one of the four variables λN, λR, μ, or β in terms of the other three. Let us now consider two special cases and one general case:
Extraction
In the case of the extraction of a naturally occurring energy source such as petroleum, HN = HR, SN = SR, and EN = ER; however, the emergy MN is less than the emergy of MR by the amount of the losses, namely
![]()
Since μ = 1,
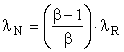
and, in the case of petroleum from a West Texas well, λN is slightly less than λR. If, on the other hand, the petroleum were from the tar sands of Utah with an EROI of 2.0, say, λN would be one-half of λR. Thus, transformity depends crucially upon EROI.
Solar or Wind Energy
If the product is single-phase, 60 Hz, 110-volt AC electricity, λR = 1.0. The availability of the sunlight that must be intercepted to produce one kilowatt hour of electricity is very large; so, μ is large. If the EROI, β, is known,
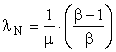
and λN will be very small. The cost of the sunshine is zero, which is a small number; but, the cost of the solar collector, the area of which must be large to intercept μ kWhrs of sunshine, is not small. Similar considerations apply to wind energy.
Fuel from Biomass
We shall need to deal with all four variables, λN, λR, μ, and β, to describe the conversion of biomass to motor fuel. The general equation applies, namely,
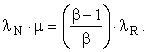
Presumably, β, the EROI, is close to two and μ is large; therefore, the relative transformity,t, where
![]()
is very small. Thus, we expect to harvest a great deal of biomass to obtain a kWhr of single-phase, 60 Hz, 110-volt AC electricity. The effect upon greenhouse gases is close to zero over an extended period; but, the area of the land required to meet any appreciable fraction of the energy budget of the United States, say, is large.
Efficiency
The above equations apply to existing extraction and conversion processes operating at steady state where β and μ are known. Suppose the transformity of the energy provided by Nature, λN, and the transformity λR’ obtained from the most efficient competing process are known, assuming that our process in not the most efficient. Then,
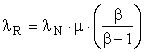
and the efficiency, η, of the process under investigation is
![]()
If our process is the most efficient, the value of the emergy of the product is changed to λR · ER.
Thomas L Wayburn
Houston, Texas
October 15, 2006