Computing Crude Birth Rates from Total Fertility Rate
Table of Contents
Age-Specific Fertility Rate (ASFR)
Time in Years Until Population Is Halved Given TFR = 1
Earlier I Computed a Halving Period that Is Too Long
Age-Specific Fertility Rate (ASFR)
![]()
where Bi = the number of live births of women in the i-th age cohort of child bearing age and Wi = the number of women in the i-th age cohort of women of childbearing age.
Total Fertility Rate (TFR)
“The Total Fertility Rate or TFR is the most powerful and useful measure of fertility in understanding a population. It represents the number of children the typical woman in that population will have over her childbearing years, based on 2 assumptions:
1. Women will have the same birth rates over their lifetimes as women in different age cohorts in that same population have had in that year; and
2. Women will survive through their childbearing years.”
– http://www.geo.hunter.cuny.edu/~imiyares/fertility.htm
![]()
where h is the number of years in an age cohort, n = the number of age cohorts of women of childbearing age, Bi = the number of live births of women in the i-th age cohort of child bearing age, and Wi = the number of women in the i-th age cohort of women of childbearing age.
Crude Birth Rate (CBR)
![]()
where B = number of live births in a given year and Bi = the number of live births of women in the i-th age cohort of childbearing age.
![]()
where P is the total number of people in the population.
No doubt the terms 'pyramidal population distribution' and 'cylindrical population distribution' are sufficiently evocative. The US has a cylindrical population distribution, which is to say that each age cohort is approximately the same size. In a mature society that does not tolerate Die-Off, every woman who reaches child bearing age lives at least until she exceeds childbearing age. Thus, we may replace Wi by Wavg in the denominator of the equation for TFR:
![]()
or
![]()
Thus,
![]()
Data for United States, 2001
Table 1. Population, Female Populations by age cohorts, and Live Births by age cohorts, 2001.
Total population 284,796,887 4,025,933
Females 10-14 10,185,198 7,781
Females 15-19 9,843,981 445,944
Females 20-24 9,619,230 1,021,627
Females 25-29 9,333,209 1,058,265
Females 30-34 10,260,525 942,697
Females 35-39 11,138,324 451,723
Females 40-44 11,477,432 92,813
Females 45-49 10,544,119 5,083
Source: National Vital Statistics Reports, Vol. 51, No. 4, February 6, 2003, Tables 2, 11.
B = 4.026 million
P = 285 million
Wavg = 10.3 million
h = 5
TFR = 2.033
Time in Years Until Population Is Halved Given TFR = 1
Peter D. Johnson of the US Census Bureau, International Programs Center, did a simulation using the International Data Base program of which he is an author. He writes, “This shows the U.S. population dropping to half the 2005 population by about 2128 if the TFR drops to 1.0 immediately or by 2142 if the TFR drops to 1.0 by 2025. In contrast, the world population would be halved by 2079 if the TFR were immediately cut to 1.0 or by 2094 if the TFR dropped to 1.0 by 2025. The reason the U.S. takes longer is because of the assumed migration which offsets some of the losses due to the fertility declines.” He sent the following figures along with tables of data and many more figures in Excel files:
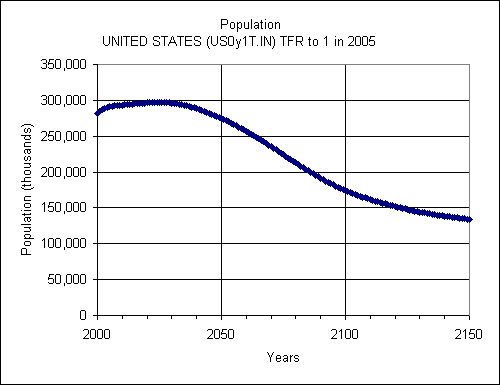
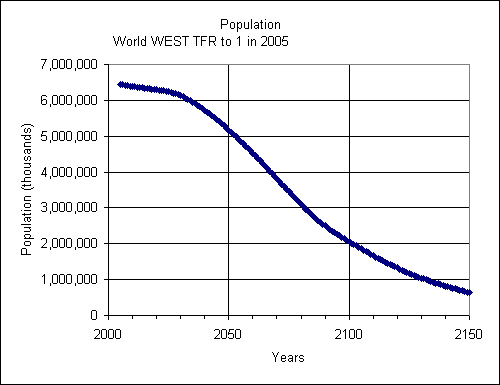
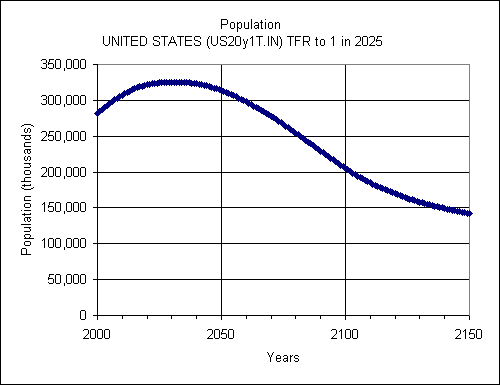

Earlier I Computed a Halving Period that Is Too Long
Note. I was looking for a best-case solution to the problem of Die-Off in the United States due to Peak Oil given that the entire population becomes rational overnight. This was found to be rather a long time, therefore I neglected the plateau that would exist in many other countries, especially in the Third World due to a pyramidal population distribution of age cohorts. I assumed that after forty years no further death of women of childbearing age occurred. The same techniques that I applied to the United States in this exercise were applied to the world population of 6.4 billion. Unfortunately, I left the crude death rate and the relative size of the cohorts of women of childbearing age constant, which is true only when the size of the population is nearly constant, i.e., for TFR about two. The following shows the steps to the wrong answer:
P2 = P1 exp{rN} = P1 exp{(b – d) N}.
Let
![]()
and
![]()
Then, for TFR = 1,
ln ρ = (b-d) N = (α TFR – d)N = ( 0.0072281 – 0.0083) N = -0.0010719 N,
where I assumed that the proportion of women of childbearing age in the general population will not change. Then, for ρ = 0.5, I obtained
![]()
By computing the crude birth rate, b, from minimum and maximum values for Wavg, I bracketed the correct solution by 390.8 years < N1/2 < 744.1. Next, I used the value of TFR = 2.033 to adjust the published value of b = 0.0141 to obtain b = 0.0141 / 2.033, b – d = r = 0.0141/2.033 – 0.0083 = -0.00136 and N1/2 = 508 years. I claimed this was a better value for N1/2, however it pointed to the same course of action (and it’s true even if the halving time is seventy-five years only); namely, we must reduce our use of high-grade energy to prevent Die-Off. No matter what else we think, this means abandoning the capitalist-style market economy and its associated modes of production and distribution of goods and services as the energetic overhead and other requirements are too great. I have indicated why this is true in “Energy in a Natural Economy” as discussed in “The Proposition that Conservation Is a Bad Thing as an Example of Reductio ad Absurdum” and I resolve to do a better job of proving it is true in the coming new year.
Houston, Texas
December 24, 2004
Revised January 1, 2005